题目内容
已知双曲线 的焦点F到一条渐近线的距离为
的焦点F到一条渐近线的距离为 ,点O为坐标原点,则此双曲线的离心率为________.
,点O为坐标原点,则此双曲线的离心率为________.
2
分析:利用已知条件和点到直线的距离公式可得点F到此条渐近线的距离为 ,经过化简可得a、b的关系式,再利用离心率的计算公式即可得出.
,经过化简可得a、b的关系式,再利用离心率的计算公式即可得出.
解答:取焦点F(c,0),一条渐近线 ,
,
则点F到此条渐近线的距离为 ,
,
化为2b= c,两边平方得4b2=3c2=3(a2+b2),
c,两边平方得4b2=3c2=3(a2+b2),
得到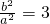 .
.
∴此双曲线的离心率e= =
= =
= =2.
=2.
故答案为2.
点评:熟练掌握双曲线的标准方程及其性质、点到直线的距离公式、离心率的计算公式是解题的关键.
分析:利用已知条件和点到直线的距离公式可得点F到此条渐近线的距离为
 ,经过化简可得a、b的关系式,再利用离心率的计算公式即可得出.
,经过化简可得a、b的关系式,再利用离心率的计算公式即可得出.解答:取焦点F(c,0),一条渐近线
 ,
,则点F到此条渐近线的距离为
 ,
,化为2b=
 c,两边平方得4b2=3c2=3(a2+b2),
c,两边平方得4b2=3c2=3(a2+b2),得到
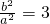 .
.∴此双曲线的离心率e=
 =
= =
= =2.
=2.故答案为2.
点评:熟练掌握双曲线的标准方程及其性质、点到直线的距离公式、离心率的计算公式是解题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 的焦点F到一条渐近线的距离为
的焦点F到一条渐近线的距离为 ,点O为坐标原点,则此双曲线的离心率为 .
,点O为坐标原点,则此双曲线的离心率为 .