题目内容
已知向量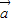 =(sinx,cosx),
=(sinx,cosx),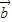 =(cosx,sinx-2cosx),0
=(cosx,sinx-2cosx),0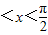 .
.(Ⅰ)若
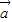 ∥
∥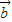 ,求x;
,求x;(Ⅱ)设f(x)=
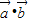 ,
,(1)求f(x)的单调增区间;
(2)函数f(x)经过怎样的平移才能使所得的图象对应的函数成为奇函数?
【答案】分析:(I)利用向量共线定理及其倍角公式,三角函数的单调性即可得出;
(II)利用数量积、两角和差的正弦公式、单调性、图象的变换即可得出.
解答:解:(I)∵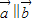 ,∴sinx(sinx-2cosx)-cos2x=0,sin2x-2sinxcosx-cos2x=0,
,∴sinx(sinx-2cosx)-cos2x=0,sin2x-2sinxcosx-cos2x=0,
∴-cos2x-sin2x=0,∴tan2x=-1.
又∵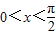 ,∴0<2x<π,∴
,∴0<2x<π,∴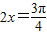 ,
,
∴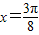 .
.
(II)f(x)=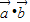 =sinxcosx+cosx(sinx-2cosx)=sin2x-2cos2x
=sinxcosx+cosx(sinx-2cosx)=sin2x-2cos2x
=sin2x-cos2x-1=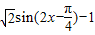 ,
,
(1)令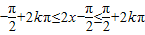 ,k∈Z,解得,
,k∈Z,解得,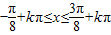 ,
,
又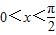 ,∴
,∴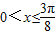 ,即(0,
,即(0,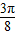 是f(x)的单调增区间.
是f(x)的单调增区间.
(2)将函数f(x)的图象向上平移1个单位,再向左平移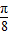 个单位,即得函数g(x)=
个单位,即得函数g(x)=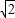 sin2x的图象,而g(x)为奇函数.
sin2x的图象,而g(x)为奇函数.
点评:熟练掌握向量共线定理及其倍角公式,三角函数的单调性、数量积、两角和差的正弦公式、单调性、图象的变换是解题的关键.
(II)利用数量积、两角和差的正弦公式、单调性、图象的变换即可得出.
解答:解:(I)∵
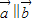 ,∴sinx(sinx-2cosx)-cos2x=0,sin2x-2sinxcosx-cos2x=0,
,∴sinx(sinx-2cosx)-cos2x=0,sin2x-2sinxcosx-cos2x=0,∴-cos2x-sin2x=0,∴tan2x=-1.
又∵
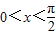 ,∴0<2x<π,∴
,∴0<2x<π,∴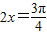 ,
,∴
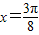 .
.(II)f(x)=
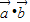 =sinxcosx+cosx(sinx-2cosx)=sin2x-2cos2x
=sinxcosx+cosx(sinx-2cosx)=sin2x-2cos2x=sin2x-cos2x-1=
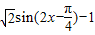 ,
,(1)令
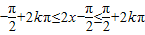 ,k∈Z,解得,
,k∈Z,解得,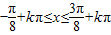 ,
,又
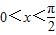 ,∴
,∴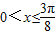 ,即(0,
,即(0,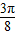 是f(x)的单调增区间.
是f(x)的单调增区间.(2)将函数f(x)的图象向上平移1个单位,再向左平移
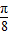 个单位,即得函数g(x)=
个单位,即得函数g(x)=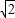 sin2x的图象,而g(x)为奇函数.
sin2x的图象,而g(x)为奇函数.点评:熟练掌握向量共线定理及其倍角公式,三角函数的单调性、数量积、两角和差的正弦公式、单调性、图象的变换是解题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知向量
=(sinx,cosx),向量
=(1,
),则|
+
|的最大值为( )
| a |
| b |
| 3 |
| a |
| b |
| A、3 | ||
B、
| ||
| C、1 | ||
| D、9 |