题目内容
函数 满足
满足 ,那么函数
,那么函数 的图象大致为( )
的图象大致为( )
C
解析试题分析:根据题意,由于函数 满足
满足 ,代入点可知
,代入点可知 ,那么函数
,那么函数
即为|  |,结合对数函数先左移一个单位,再将x轴下方的关于x轴对称变换可知,图象为C。
|,结合对数函数先左移一个单位,再将x轴下方的关于x轴对称变换可知,图象为C。
考点:函数的图象
点评:主要是考查了对数函数图象的表示,属于基础题。

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
若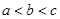 ,则函数
,则函数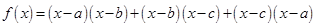 的两个零点分别位于区间( )
的两个零点分别位于区间( )
A. 和 和 内 内 |
B.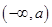 和 和 内 内 |
C. 和 和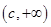 内 内 |
D.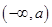 和 和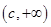 内 内 |
函数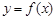 的图像如图所示,在区间
的图像如图所示,在区间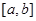 上可找到
上可找到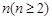 个不同的数
个不同的数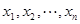 ,使得
,使得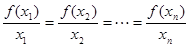 ,则
,则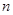 的取值范围为( )
的取值范围为( )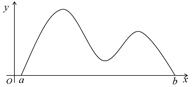
A.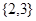 | B.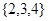 |
C.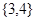 | D.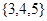 |
已知 是定义在R上的奇函数,若对于x≥0,都有f(x+2)=
是定义在R上的奇函数,若对于x≥0,都有f(x+2)= ,且
,且
当 时,
时, ,则
,则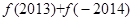 =( )
=( )
| A.1-e | B.e-1 | C.-l-e | D.e+l |
若函数 在
在 是增函数,则a的取值范围是( )
是增函数,则a的取值范围是( )
A. | B. | C. | D. |
已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)等于( )
| A.4 | B.3 | C.2 | D.1 |
 和
和 ,动点
,动点 在直线
在直线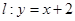 上移动,椭圆
上移动,椭圆 以
以 为焦点且经过点
为焦点且经过点 ,记椭圆
,记椭圆 ,则函数
,则函数 的大致图像( )
的大致图像( )
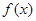 (
( R)满足
R)满足 ,
, ,则函数
,则函数 的图像是( )
的图像是( ) 



 的图象大致为( )
的图象大致为( )