题目内容
(2013•黄浦区二模)一厂家向用户提供的一箱产品共10件,其中有1件次品.用户先对产品进行随机抽检以决定是否接受.抽检规则如下:至多抽检3次,每次抽检一件产品(抽检后不放回),只要检验到次品就停止继续抽检,并拒收这箱产品;若3次都没有检验到次品,则接受这箱产品,按上述规则,该用户抽检次数的数学期望是
.
| 27 |
| 10 |
| 27 |
| 10 |
分析:设ξ表示该用户抽检次数,ξ的取值可能为1,2,3.利用古典概型的概率计算公式和概率的性质、随机变量的分布列和数学期望即可得出.
解答:解:设ξ表示该用户抽检次数,ξ的取值可能为1,2,3.
若抽到第一件产品为次品即停止检查,则P(ξ=1)=
.
若抽到第一件产品为正品,第二件品为次品即停止检查,则P(ξ=2)=
×
=
.
第3次无论抽到正品还是次品都停止检查,则P(ξ=3)=1-P(ξ=1)-P(ξ=2)=
.
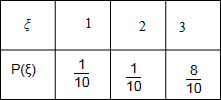
故ξ的分布列为
∴Eξ=1×
+2×
+3×
=
.
故答案为
.
若抽到第一件产品为次品即停止检查,则P(ξ=1)=
| 1 |
| 10 |
若抽到第一件产品为正品,第二件品为次品即停止检查,则P(ξ=2)=
| 9 |
| 10 |
| 1 |
| 9 |
| 1 |
| 10 |

第3次无论抽到正品还是次品都停止检查,则P(ξ=3)=1-P(ξ=1)-P(ξ=2)=
| 8 |
| 10 |
故ξ的分布列为
∴Eξ=1×
| 1 |
| 10 |
| 1 |
| 10 |
| 8 |
| 10 |
| 27 |
| 10 |
故答案为
| 27 |
| 10 |
点评:熟练掌握古典概型的概率计算公式和概率的性质、随机变量的分布列和数学期望是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目