Question

20．已知二次函数f（x）=ax²+bx+c（x∈R，a≠0）．
（1）若a=1，b=-4，c=3，求f（x）＜0的解集．
（2）若a＜0，c=-2，方程f（x）=x的两实根x₁，x₂满足x₁∈（0，1），x₂∈（1，2）．求证：-4＜$\frac{b}{a}$＜-1．
（3）若函数f（x）的最小值为0，且a＜b，求$\frac{a+2b+4c}{b-a}$的最小值．

Answer 1

分析 （1）a=1，b=-4，c=3，f（x）=x²-4x+3，由f（x）＜0，化为（x-1）（x-3）＜0．解出即可得出．
（2）方程f（x）=x化为g（x）=ax²+（b-1）x-2=0，（a＜0），方程f（x）=x的两实根x₁，x₂满足x₁∈（0，1），x₂∈（1，2）．可得$\left\{\begin{array}{l}{g（0）＜0}\\{g（1）＞0}\\{g（2）＜0}\end{array}\right.$，即$\left\{\begin{array}{l}{a+b-3＞0}\\{2a+b-2＜0}\end{array}\right.$，如图所示阴影部分，P（-1，4）．利用斜率的意义即可得出．
（3）f（x）=$a（x+\frac{b}{2a}）^{2}+$$\frac{4ac-{b}^{2}}{4a}$，由函数f（x）的最小值为0，且a＜b，可得0＜a＜b，b²=4ac．令$\frac{b}{a}=t＞1$，$\frac{a+2b+4c}{b-a}$=$\frac{a+2b+\frac{{b}^{2}}{a}}{b-a}$=$\frac{{t}^{2}+2t+1}{t-1}$=$t-1+\frac{4}{t-1}$+4，利用基本不等式的性质即可得出．

解答 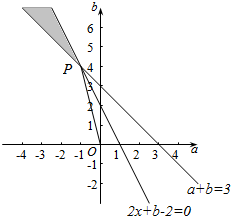（1）解：a=1，b=-4，c=3，f（x）=x²-4x+3，由f（x）＜0，化为（x-1）（x-3）＜0．解得1＜x＜3，
∴f（x）＜0的解集是{x|1＜x＜3}．
（2）证明：方程f（x）=x化为g（x）=ax²+（b-1）x-2=0，（a＜0），
∵方程f（x）=x的两实根x₁，x₂满足x₁∈（0，1），x₂∈（1，2）．
∴$\left\{\begin{array}{l}{g（0）＜0}\\{g（1）＞0}\\{g（2）＜0}\end{array}\right.$，即$\left\{\begin{array}{l}{-2＜0}\\{a+b-3＞0}\\{4a+2b-4＜0}\end{array}\right.$，化为$\left\{\begin{array}{l}{a+b-3＞0}\\{2a+b-2＜0}\end{array}\right.$，
如图所示阴影部分，P（-1，4）．
k_OP=-4，∴$-4＜\frac{b}{a}＜-1$．
（3）解：f（x）=$a（x+\frac{b}{2a}）^{2}+$$\frac{4ac-{b}^{2}}{4a}$，
∵函数f（x）的最小值为0，且a＜b，
∴0＜a＜b，b²=4ac．
令$\frac{b}{a}=t＞1$，
$\frac{a+2b+4c}{b-a}$=$\frac{a+2b+\frac{{b}^{2}}{a}}{b-a}$=$\frac{{t}^{2}+2t+1}{t-1}$=$t-1+\frac{4}{t-1}$+4≥2$\sqrt{（t-1）•\frac{4}{t-1}}$+4=8，当且仅当t=3即b=3a＞0时取等号．
∴$\frac{a+2b+4c}{b-a}$的最小值为8．

点评 本题考查了二次函数的性质、一元二次不等式解法、线性规划、斜率的意义、基本不等式的性质，考查了推理能力与计算能力，属于中档题．