题目内容
已知函数f（x）=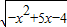
的定义域为集合A，函数g（x）=x-a（0≤x≤4）的值域为集合B．（Ⅰ）求集合A；
（Ⅱ）若集合A，B满足A∩B=A，求实数a的取值范围．
【答案】分析：（Ⅰ）由-x2+5x-4≥0可解得A；（Ⅱ）由A∩B=A，得A⊆B，借助数轴可得关于a的不等式组，解出即可；
解答：解：（Ⅰ）由-x2+5x-4≥0，解得1≤x≤4，所以A={x|1≤x≤4}；
（Ⅱ）因为A∩B=A，所以A⊆B，
所以-a≤1且4-a≥4，解得-1≤a≤0，
故实数a的取值范围是[-1，0]．
点评：本题考查一元二次不等式的解法、集合关系中的参数问题，属基础题．
解答：解：（Ⅰ）由-x2+5x-4≥0，解得1≤x≤4，所以A={x|1≤x≤4}；
（Ⅱ）因为A∩B=A，所以A⊆B，
所以-a≤1且4-a≥4，解得-1≤a≤0，
故实数a的取值范围是[-1，0]．
点评：本题考查一元二次不等式的解法、集合关系中的参数问题，属基础题．
练习册系列答案
相关题目
已知函数f（x）=x3的切线的斜率等于1，则这样的切线有（ ）
| A、1条 | B、2条 | C、3条 | D、不确定 |