题目内容
函数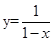 的图像与函数
的图像与函数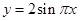 (
(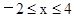 )的图像所有交点的横坐标之和等于( )
)的图像所有交点的横坐标之和等于( )
A.2 B.4 C.6 D.8
【答案】
D
【解析】
试题分析:令 ,则
,则 ;则
;则 化为
化为 ,
, 化为
化为 .
.
因为, ,所以,
,所以, ,即
,即 .
. ,
, 均为
均为 上的奇函数,令
上的奇函数,令 ,若有
,若有 使得
使得 ,则必有
,则必有 也使
也使 成立.
成立.
此时, 的值分别为
的值分别为 ,他们的和为2。另外由于
,他们的和为2。另外由于 有意义,故z≠0,排除了交点为奇数个的情形。问题转化为求
有意义,故z≠0,排除了交点为奇数个的情形。问题转化为求 在
在 上的零点有几对的问题。画出
上的零点有几对的问题。画出 ,
, 的图像,
的图像,

交点共有四对,横坐标之和为8,故选D..
考点:函数的图象,函数方程,函数的奇偶性.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
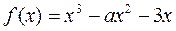 .
.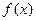 在
在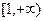 上是增函数, 求实数a的取值范围.
上是增函数, 求实数a的取值范围.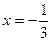 是
是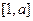 上的最大值;
上的最大值;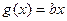 的图像与函数
的图像与函数 的图像与函数
的图像与函数 的图像的交点个数为( )
的图像的交点个数为( )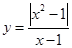 的图像与函数
的图像与函数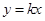 的图像恰有两个交点,则实数
的图像恰有两个交点,则实数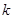 的取值范围是 .
的取值范围是 .