题目内容
已知函数![]() (
(![]() 为实常数).
为实常数).
(1)若![]() ,作函数
,作函数![]() 的图像;
的图像;
(2)设![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)设![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围.
的取值范围.
(1)图象略 (2)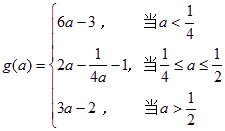
(3)![]()
解析:
(1)当![]() 时,
时,![]()
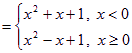 .作图(如右所示)
.作图(如右所示)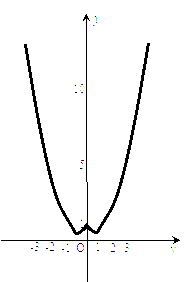
……(4分)
(2)当![]() 时,
时,![]() .
.
若![]() ,则
,则![]() 在区间
在区间![]() 上是减函数,
上是减函数,
![]() .……(5分)
.……(5分)
若![]() ,则
,则![]() ,
,![]() 图像的对称轴是直线
图像的对称轴是直线![]() .
.
当![]() 时,
时,![]() 在区间
在区间![]() 上是减函数,
上是减函数,![]() .……(6分)
.……(6分)
当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上是增函数,
上是增函数,
![]() .……(7分)
.……(7分)
当![]() ,即
,即![]() 时,
时,![]() ,……(8分)
,……(8分)
当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上是减函数,
上是减函数,
![]() .……(9分)
.……(9分)
综上可得![]()
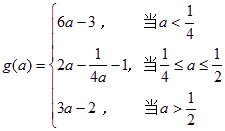 .……(10分)
.……(10分)
(3)当![]() 时,
时,![]() ,在区间
,在区间![]() 上任取
上任取![]() ,
,![]() ,且
,且![]() ,
,
则
![]() .……(12分)
.……(12分)
因为![]() 在区间
在区间![]() 上是增函数,所以
上是增函数,所以![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() ,
,
当![]() 时,上面的不等式变为
时,上面的不等式变为![]() ,即
,即![]() 时结论成立.……(13分)
时结论成立.……(13分)
当![]() 时,
时,![]() ,由
,由![]() 得,
得,![]() ,解得
,解得![]() ,…(14分)
,…(14分)
当![]() 时,
时,![]() ,由
,由![]() 得,
得,![]() ,解得
,解得![]() ,(15分)
,(15分)
所以,实数![]() 的取值范围为
的取值范围为![]() .……(16分)
.……(16分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
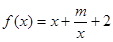 (
(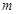 为实常数).
为实常数). 图像上动点
图像上动点 到定点
到定点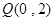 的距离的最小值为
的距离的最小值为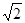 ,求实数
,求实数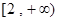 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数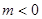 ,若不等式
,若不等式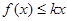 在
在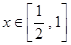 有解,求
有解,求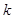 的取值范围.
的取值范围.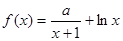 (
(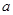 为实常数)的两个极值点为
为实常数)的两个极值点为 ,且满足
,且满足
 与
与 的大小.
的大小.