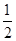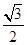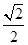题目内容
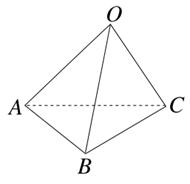
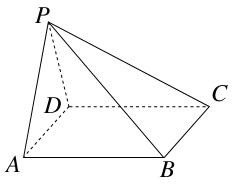
如图,三棱柱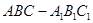 的各棱长均为2,侧棱
的各棱长均为2,侧棱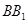 与底面
与底面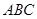 所成的角为
所成的角为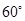 ,
,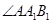 为锐角,且侧面
为锐角,且侧面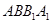 ⊥底面
⊥底面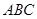 ,给出下列四个结论:
,给出下列四个结论: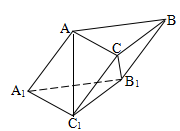
①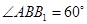 ;
;
②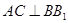 ;
;
③直线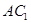 与平面
与平面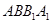 所成的角为
所成的角为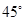 ;
;
④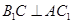 .
.
其中正确的结论是( )
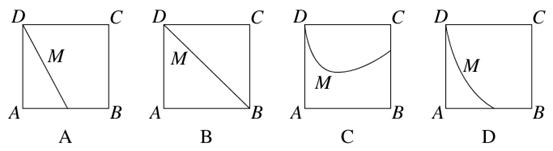
| A.①③ | B.②④ | C.①③④ | D.①②③④ |
C.
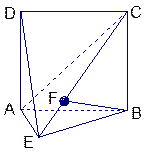
解析试题分析:如图过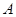 作
作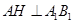 ,
,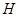 为垂足,连结
为垂足,连结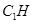 ,如图建立空间直角坐标系,①:∵侧棱
,如图建立空间直角坐标系,①:∵侧棱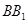 与底面
与底面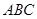 所成的角为
所成的角为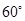 ,
,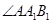 为锐角,侧面
为锐角,侧面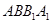 ⊥底面
⊥底面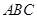 ,∴
,∴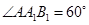 ,又由三棱柱各棱长相等,可知四边形
,又由三棱柱各棱长相等,可知四边形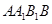 为菱形,∴
为菱形,∴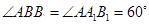 ,∴①正确;②:易知
,∴①正确;②:易知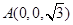 ,
,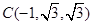 ,
,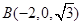 ,
,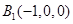 ∴
∴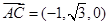 ,
,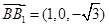 ,∴
,∴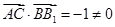 ,∴②错误;③:由题意得
,∴②错误;③:由题意得 即为
即为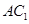 与平面
与平面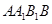 所成的角,
所成的角,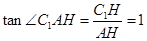 ,
,
∴ ,∴③正确;④:由②,
,∴③正确;④:由②,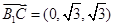 ,
,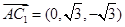 ,∴
,∴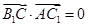 ,∴
,∴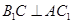 ,∴④正确.
,∴④正确.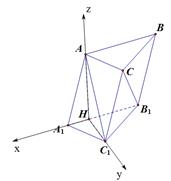
考点:1.线面角与面面角的求解;2.空间向量证明线线垂直.

练习册系列答案
相关题目
已知点A(-3,1,4),则点A关于x轴的对称点的坐标为( )
| A.(-3,1,-4) | B.(3,-1,-4) | C.(-3,-1,-4) | D.(-3,,1,-4) |
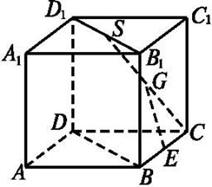
点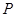 是棱长为1的正方体
是棱长为1的正方体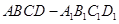 内一点,且满足
内一点,且满足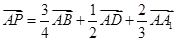 ,则点
,则点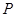 到棱
到棱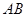 的距离为
的距离为
A.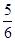 | B.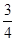 | C.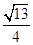 | D.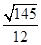 |
已知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的一个单位法向量是( )
A.( , , ,- ,- ) ) | B.( ,- ,- , , ) ) | C.(- , , , , ) ) | D.(- ,- ,- ,- ,- ) ) |
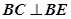 ;
; 与平面
与平面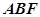 所成角的正弦值.
所成角的正弦值.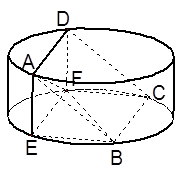
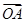 、
、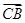 夹角θ的余弦值为( )
夹角θ的余弦值为( )