题目内容
已知函数 .
.
(1)求f(x)的定义域与值域(用区间表示) (2)求证f(x)在 上递减.
上递减.
解:(1)要使函数有意义,则4x+1≠0,解得 .
.
所以原函数的定义域是 .
. ,
,
所以值域为 .
.
(2)在区间 上任取x1,x2,且x1<x2,则
上任取x1,x2,且x1<x2,则
∵x1<x2,∴x2-x1>0
又 ,∴4x1+1>0,4x2+1>0,
,∴4x1+1>0,4x2+1>0,
∴f(x1)-f(x2)>0∴f(x1)>f(x2),
∴函数f(x)在 上递减.
上递减.
分析:求定义域时要满足分母不能是0,即4x+1≠0
求函数f(x)的值域用分离常数法,想办法把分子上的x消掉,即, =
=
证明一个函数递减时可用定义法来证.
点评:函数的定义域、值域和单调性是考查的重点内容,尤其是证明函数单调性的定义法要掌握.
 .
.所以原函数的定义域是
 .
. ,
,所以值域为
 .
.(2)在区间
 上任取x1,x2,且x1<x2,则
上任取x1,x2,且x1<x2,则
∵x1<x2,∴x2-x1>0
又
 ,∴4x1+1>0,4x2+1>0,
,∴4x1+1>0,4x2+1>0,∴f(x1)-f(x2)>0∴f(x1)>f(x2),
∴函数f(x)在
 上递减.
上递减.分析:求定义域时要满足分母不能是0,即4x+1≠0
求函数f(x)的值域用分离常数法,想办法把分子上的x消掉,即,
 =
=
证明一个函数递减时可用定义法来证.
点评:函数的定义域、值域和单调性是考查的重点内容,尤其是证明函数单调性的定义法要掌握.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.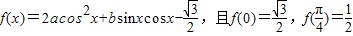 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.