题目内容
如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点.(1)求证:A1B∥平面ADC1;
(2)求二面角C1-AD-C的余弦值;
(3)试问线段A1B上是否存在点E,使C1E与平面ADC1成30°角?若存在,确定E点位置,若不存在,说明理由.
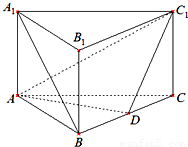
【答案】分析:(1)利用直三棱柱的性质、三角形的中位线定理、线面平行的判定定理即可得出;
(2)由 ABC-A1B1C1是直三棱柱,且∠ABC=90°,故BA,BC,BB1两两垂直.如图建立空间直角坐标系B-xyz.利用两个平面的法向量的夹角即可得出二面角;
(3)利用线面角的夹角公式即可得出.
解答:(1)证明:连接A1C,交AC1于点O,连接OD.
由 ABC-A1B1C1是直三棱柱,得四边形ACC1A1为矩形,O为A1C的中点.
又D为BC中点,∴OD为△A1BC中位线,
∴A1B∥OD.
∵OD?平面ADC1,A1B?平面ADC1,∴A1B∥平面ADC1.
(2)解:由 ABC-A1B1C1是直三棱柱,且∠ABC=90°,故BA,BC,BB1两两垂直.
如图建立空间直角坐标B-xyz.
设BA=2,则B(0,0,0),C(2,0,0),A(0,2,0),C1(2,0,1),D(1,0,0).
所以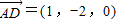 ,
,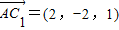
设平面ADC1的法向量为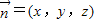 ,则
,则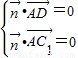 ,
,
所以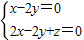 ,取y=1,得
,取y=1,得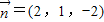 .
.
易知平面ADC的法向量为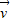 =(0,0,1).
=(0,0,1).
由二面角C1-AD-C是锐角,得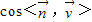 =
=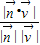 =
= .
.
所以二面角C1-AD-C的余弦值为 .
.
(3)解:假设存在满足条件的点E,设E(0,a,b).
∵E在线段A1B上,由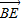 =
=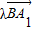 且其中0≤λ≤1,
且其中0≤λ≤1,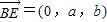
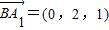
即(0,a,b)=λ(0,2,1),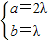 ,E(0,2λ,λ).
,E(0,2λ,λ).
∴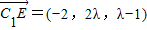 ,
,
以由(2)知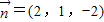 ,∵
,∵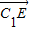 与平面ADC1成30角,
与平面ADC1成30角,
∴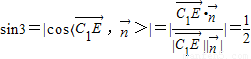 .
.
即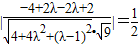 ,
,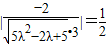 ,
,
化为45λ2-18λ+29=0,
∵△<0,∴方程无解.
所以在线段A1B上不存在点E.
点评:熟练掌握直三棱柱的性质、三角形的中位线定理、线面平行的判定定理、通过建立空间直角坐标系B-xyz并利用两个平面的法向量的夹角求二面角、线面角的夹角公式等是解题的关键..
(2)由 ABC-A1B1C1是直三棱柱,且∠ABC=90°,故BA,BC,BB1两两垂直.如图建立空间直角坐标系B-xyz.利用两个平面的法向量的夹角即可得出二面角;
(3)利用线面角的夹角公式即可得出.
解答:(1)证明:连接A1C,交AC1于点O,连接OD.
由 ABC-A1B1C1是直三棱柱,得四边形ACC1A1为矩形,O为A1C的中点.
又D为BC中点,∴OD为△A1BC中位线,
∴A1B∥OD.
∵OD?平面ADC1,A1B?平面ADC1,∴A1B∥平面ADC1.
(2)解:由 ABC-A1B1C1是直三棱柱,且∠ABC=90°,故BA,BC,BB1两两垂直.
如图建立空间直角坐标B-xyz.
设BA=2,则B(0,0,0),C(2,0,0),A(0,2,0),C1(2,0,1),D(1,0,0).
所以
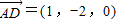 ,
,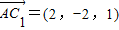
设平面ADC1的法向量为
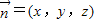 ,则
,则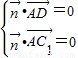 ,
,所以
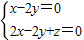 ,取y=1,得
,取y=1,得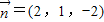 .
.易知平面ADC的法向量为
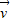 =(0,0,1).
=(0,0,1).由二面角C1-AD-C是锐角,得
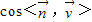 =
=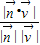 =
= .
.所以二面角C1-AD-C的余弦值为
 .
.(3)解:假设存在满足条件的点E,设E(0,a,b).
∵E在线段A1B上,由
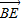 =
=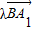 且其中0≤λ≤1,
且其中0≤λ≤1,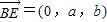
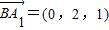
即(0,a,b)=λ(0,2,1),
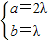 ,E(0,2λ,λ).
,E(0,2λ,λ).∴
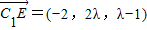 ,
,以由(2)知
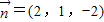 ,∵
,∵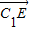 与平面ADC1成30角,
与平面ADC1成30角,∴
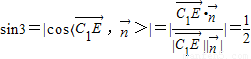 .
.即
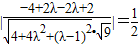 ,
,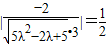 ,
,化为45λ2-18λ+29=0,
∵△<0,∴方程无解.
所以在线段A1B上不存在点E.
点评:熟练掌握直三棱柱的性质、三角形的中位线定理、线面平行的判定定理、通过建立空间直角坐标系B-xyz并利用两个平面的法向量的夹角求二面角、线面角的夹角公式等是解题的关键..

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目




