题目内容
已知圆方程为 .
.
(1)求圆心轨迹的参数方程C;
(2)点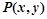 是(1)中曲线C上的动点,求
是(1)中曲线C上的动点,求 的取值范围.
的取值范围.
【答案】
(1) ; (2) -
; (2) - ≤2x+y≤
≤2x+y≤
【解析】1)先将圆的一般式方程转化成圆的标准方程,从而求出圆心的参数方程;
(2)利用参数方程将2x+y表示成8cosθ+3sinθ,然后利用辅助角公式求出8cosθ+3sinθ的取值范围即可.
将圆的方程整理得:(x-4cos )2+(y-3sin
)2+(y-3sin )2=1
设圆心坐标为P(x,y)
)2=1
设圆心坐标为P(x,y)
则
(2)2x+y=8cos +3sin
+3sin
= ∴ -
∴ - ≤2x+y≤
≤2x+y≤

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
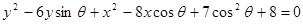 .
.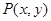 是(1)中曲线C上的动点,求
是(1)中曲线C上的动点,求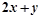 的取值范围.
的取值范围.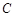 方程为:
方程为: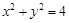 .
.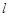 过点
过点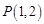 ,且与圆
,且与圆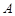 、
、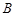 两点,若
两点,若 ,求直线
,求直线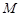 作平行于
作平行于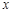 轴的直线
轴的直线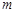 ,设
,设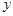 轴的交点为
轴的交点为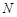 ,若向量
,若向量 (
(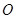 为原点),求动点
为原点),求动点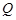 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.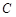 方程为:
方程为: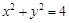 .
.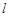 过点
过点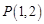 ,且与圆
,且与圆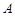 、
、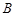 两点,若
两点,若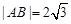 ,求直线
,求直线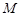 作平行于
作平行于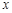 轴的直线
轴的直线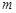 ,设
,设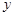 轴的交点为
轴的交点为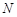 ,若向量
,若向量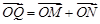 ,求动点
,求动点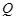 的轨迹方程。
的轨迹方程。