Question

【题目】已知圆经过两点，且圆心在直线上，直线的方程为。

（1）求圆的方程；

（2）证明：直线与圆恒相交；

（3）求直线被圆截得的弦长的取值范围。

Answer 1

【答案】（1）；（2）证明见解析；（3）

【解析】

（1）设圆的一般方程，将PQ点代入方程，将圆心代入直线，解方程组，即可。

（2）求出直线：过定点，说明点M在圆内，即可。

（3）当直线过圆心时弦长有最大值10,

当直线与过圆心与定点的直线垂直时有最小值。

（1）设圆的方程为，

由条件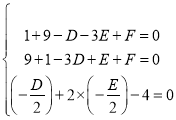得，解得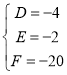

∴圆的方程为；

（2）由，得，

令，

得，即直线过定点，

由，知点在圆内，

∴直线与圆恒相交。

（3）圆心，半径为5，由题意知，当点满足垂直于直线时，弦长最短，

直线被圆心截得的最短弦长为，

直径最长10，弦长的取值范围为。