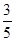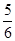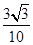题目内容
若向量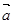 、
、 的坐标满足
的坐标满足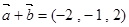 ,
,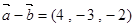 ,则
,则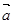 ·
· 等于
等于
A. | B.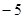 | C.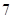 | D.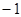 |
B
解析试题分析:因为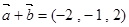 ,
,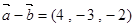 ,所以
,所以 所以
所以
考点:本小题注意考查向量的坐标运算.
点评:向量的坐标运算是高考经常考查的内容,难度一般较低,灵活运用公式计算即可.

练习册系列答案
相关题目
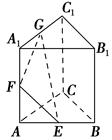
棱长均为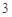 三棱锥
三棱锥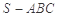 ,若空间一点
,若空间一点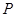 满足
满足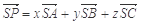
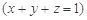 则
则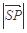 的最小值为( )
的最小值为( )
A.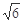 | B.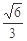 | C.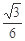 | D.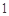 |
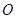 是坐标原点,设
是坐标原点,设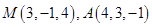 ,若
,若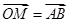 ,则点
,则点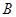 的坐标应为( )
的坐标应为( )
A.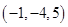 | B.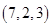 | C.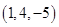 | D.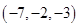 |
若向量a=(1,l,2),b=(2,-1,2),a、b夹角的余弦值为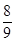 ,则l=( )
,则l=( )
| A.2 | B.-2 | C.-2或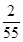 | D.2或-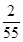 |
到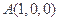 的距离除以到
的距离除以到 的距离的值为
的距离的值为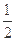 的点
的点 的坐标满足( )
的坐标满足( )
A. |
B.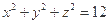 |
C.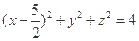 |
D. |
若向量a=(1,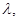 0),b=(2,0,0)且a与b的夹角为
0),b=(2,0,0)且a与b的夹角为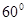 ,则
,则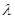 等于
等于
| A.1 | B. |
C.- 或 或 | D.-1或1 |
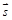 =(-1,1,1),平面π的法向量为
=(-1,1,1),平面π的法向量为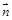 =(2,x2+x,-x),若直线l∥平面π,则x的值为___________.
=(2,x2+x,-x),若直线l∥平面π,则x的值为___________.