题目内容
设椭圆 的离心率为
的离心率为 ,焦点在x轴上且长轴长为30.若曲线
,焦点在x轴上且长轴长为30.若曲线 上的点到椭圆
上的点到椭圆 的两个焦点的距离的差的绝对值等于10,则曲线
的两个焦点的距离的差的绝对值等于10,则曲线 的标准方程为( )
的标准方程为( )
A. | B. | C. | D. |
B
解析试题分析:椭圆 的离心率为
的离心率为 ,焦点在x轴上且长轴长为30,所以
,焦点在x轴上且长轴长为30,所以 所以曲线
所以曲线 的两个焦点为(-7,0),(7,0),并且c=7,a=5,所以
的两个焦点为(-7,0),(7,0),并且c=7,a=5,所以 ,所以曲线
,所以曲线 的标准方程为
的标准方程为 .
.
考点:椭圆的标准方程及几何性质,双曲线的定义及标准方程.
点评:掌握椭圆及双曲线的标准方程及其几何性质是解决此问题的关键,本小题属于容易题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是椭圆
是椭圆 的两个焦点,
的两个焦点, 为椭圆上一点,且
为椭圆上一点,且 ,则
,则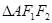 的面积为
的面积为
| A.7 | B. | C. | D. |
过点 且与双曲线
且与双曲线 -y
-y =1有公共渐近线的双曲线方程是( )
=1有公共渐近线的双曲线方程是( )
A. - -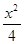 =1 =1 | B. - - =1 =1 |
C.y - - =1 =1 | D. - -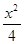 =1或 =1或 - - =1 =1 |
椭圆 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
抛物线 的焦点到准线的距离为( )
的焦点到准线的距离为( )
| A.1 | B. | C. | D.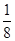 |
抛物线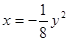 的焦点坐标是( )
的焦点坐标是( )
A. | B.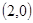 | C. | D. |
椭圆 的离心率是( )
的离心率是( )
A. | B.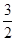 | C. | D. |
若方程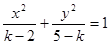 表示双曲线,则实数k的取值范围是( )
表示双曲线,则实数k的取值范围是( )
| A.2<k<5 ; | B.k>5 ; |
| C.k<2或k>5; | D.以上答案均不对 |
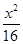 +
+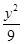 =1的两焦点,过点F2的直线交椭圆于A,B两点.在△AF1B中,若有两边之和是10,则第三边的长度为 ( )
=1的两焦点,过点F2的直线交椭圆于A,B两点.在△AF1B中,若有两边之和是10,则第三边的长度为 ( )