题目内容
【题目】狄利克雷是德国著名数学家，函数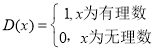
，被称为狄利克雷函数，下面给出关于狄利克雷函数
的五个结论：
①若
是无理数，则
；
②函数的值域是
；
③函数是偶函数；
④若
且
为有理数，则
对任意的
恒成立；
⑤存在不同的三个点
，使得
为等边三角形.
其中正确结论的序号是___________.
【答案】③④⑤
【解析】
由函数解析式直接代入可判断①；由函数的解析式结合函数值域的概念可判断②；分
是无理数、是有理数分类，结合解析式即可判断③、④；取特殊点即可判断⑤；即可得解.
对于①，若是无理数，则
，故①错误；
对于②，函数
的值域为
，故②错误；
对于③，若是无理数，则
也是无理数，所以
；若是有理数，则也是有理数，所以
；所以函数是偶函数，故③正确；
对于④，因为
且
为有理数，若是无理数，则
也是无理数，所以
；若是有理数，则也是有理数，所以
；所以若且为有理数，则
对任意的
恒成立，故④正确；
对于⑤，取
，
，
，可得
，
，
.
∴
，
，
，
恰好为等边三角形，故⑤正确.
故答案为：③④⑤.
【题目】某同学用“五点法”画函数
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数
的解析式;
(2)把
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
个单位长度,得到函数
的图象,求
的值.
【题目】某校组织了一次新高考质量测评，在成绩统计分析中，某班的数学成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏，但可见部分如下，据此解答如下问题：
5 | 6 | 8 | ||||||||
6 | 2 | 3 | 3 | 5 | 6 | 8 | 9 | |||
7 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
8 | ||||||||||
9 | 5 | 8 |
（1）求该班数学成绩在
的频率及全班人数；
（2）根据频率分布直方图估计该班这次测评的数学平均分；
（3）若规定90分及其以上为优秀，现从该班分数在80分及其以上的试卷中任取2份分析学生得分情况，求在抽取的2份试卷中至少有1份优秀的概率.