题目内容
已知函数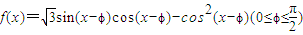 为偶函数.
为偶函数.(I)求函数的单调减区间;
(II)把函数的图象向右平移
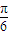 个单位(纵坐标不变),得到函数g(x)的图象,求方程
个单位(纵坐标不变),得到函数g(x)的图象,求方程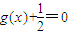 的解集.
的解集.
【答案】分析:(I)根据倍角公式和两角差的正弦公式对解析式化简,再由函数是偶函数求出φ的值,再由余弦函数的单调性和整体思想求出函数的递减区间;
(Ⅱ)由平移法则求出函数g(x)的解析式,再代入所给的方程进行求解,最后再用集合形式表示出来.
解答:解:(I)
=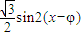 -
-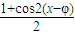 =
=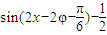 ,
,
∵f(x)为偶函数,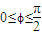 且,∴-2φ
且,∴-2φ =
= ,k∈Z,解得φ=
,k∈Z,解得φ=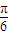 ,
,
则f(x)= =-cos2x
=-cos2x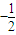 ,
,
由2kπ-π≤2x≤2kπ(k∈Z)得, ≤x≤kπ,
≤x≤kπ,
故所求的递减区间是[ ,kπ](k∈Z),
,kπ](k∈Z),
(II)函数的图象向右平移 个单位,得到函数g(x)的图象,则g(x)=-cos(2x-
个单位,得到函数g(x)的图象,则g(x)=-cos(2x-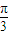 )
) ,
,
由方程 得,-cos(2x-
得,-cos(2x- )=0,即cos(2x-
)=0,即cos(2x-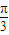 )=0,解得2x-
)=0,解得2x-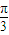 =
= (k∈Z),
(k∈Z),
即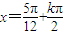 (k∈Z),
(k∈Z),
所求的解集为{x|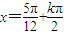 (k∈Z)}.
(k∈Z)}.
点评:本题考查了倍角公式和两角差的正弦公式,余弦函数的性质的应用,以及三角函数图象的平移问题,掌握余弦函数的基本性质和解析式正确化简,是解好本题的关键.
(Ⅱ)由平移法则求出函数g(x)的解析式,再代入所给的方程进行求解,最后再用集合形式表示出来.
解答:解:(I)

=
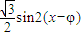 -
-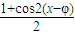 =
=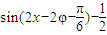 ,
,∵f(x)为偶函数,
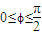 且,∴-2φ
且,∴-2φ =
= ,k∈Z,解得φ=
,k∈Z,解得φ=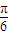 ,
,则f(x)=
 =-cos2x
=-cos2x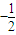 ,
,由2kπ-π≤2x≤2kπ(k∈Z)得,
 ≤x≤kπ,
≤x≤kπ,故所求的递减区间是[
 ,kπ](k∈Z),
,kπ](k∈Z),(II)函数的图象向右平移
 个单位,得到函数g(x)的图象,则g(x)=-cos(2x-
个单位,得到函数g(x)的图象,则g(x)=-cos(2x-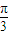 )
) ,
,由方程
 得,-cos(2x-
得,-cos(2x- )=0,即cos(2x-
)=0,即cos(2x-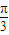 )=0,解得2x-
)=0,解得2x-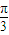 =
= (k∈Z),
(k∈Z),即
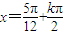 (k∈Z),
(k∈Z),所求的解集为{x|
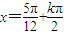 (k∈Z)}.
(k∈Z)}.点评:本题考查了倍角公式和两角差的正弦公式,余弦函数的性质的应用,以及三角函数图象的平移问题,掌握余弦函数的基本性质和解析式正确化简,是解好本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 的值。
的值。 为偶函数.
为偶函数. ,判断λ与E的关系;
,判断λ与E的关系; (m>0,n>0)时,若函数f(x)的值域为[2-3m,2-3n],求m,n的值.
(m>0,n>0)时,若函数f(x)的值域为[2-3m,2-3n],求m,n的值. 为偶函数,且函数y=f(x)图象的两相邻对称轴的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴的距离为 .
. 个单位后,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,得到函数y=g(x)的图象,求g(x)的单调递减区间. ,使不等式f(x)<m成立,求实数m的取值范围.
,使不等式f(x)<m成立,求实数m的取值范围. 为偶函数,且其图象上相邻两对称轴之间的距离为
为偶函数,且其图象上相邻两对称轴之间的距离为 .
. 的表达式。
的表达式。 ,求
,求 的值.
的值.