题目内容

已知关于x的方程tan²x-tanx-a+1=0在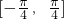 $数学公式$ 内恰有两个不相等的实数根，则a的取值范围是________．

$\text{[math]}$
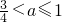
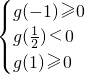分析：先由x∈[- $\text{[math]}$ ， $\text{[math]}$ ]，得tanx∈[-1，1]；令t=tanx，把问题转化为函数g（t）=t²-t-a+1在[-1，1]上恰有两个不相等的实数根，再结合一元二次方程的根的分布与系数的关系得到 $\text{[math]}$ 解之即可求a的取值范围．
解答：因为x∈[- $\text{[math]}$ ， $\text{[math]}$ ]，
∴tanx∈[-1，1]．
令t=tanx，则问题转化为函数g（t）=t²-t-a+1在[-1，1]上恰有两个不相等的实数根．
因为其对称轴为t= $\text{[math]}$ ．故须满足 $\text{[math]}$ ? $\text{[math]}$ ＜a≤1．
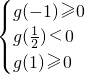故答案为： $\text{[math]}$ a≤1．
点评：本题考查一元二次方程的根的分布与系数的关系，考查分类讨论思想，转化思想，是中档题．解决本题的关键在于把问题转化为函数g（t）=t²-t-a+1在[-1，1]上恰有两个不相等的实数根．