题目内容
等差数列{an}中,已知a2≤6,a4≤4,则a3的取值范围是 .
【答案】分析:利用等差数列的性质,将a3表示a2,a4的关系,为从而确定a3的取值范围.
解答:解:在等差数列中由a2≤6,a4≤4得a2+a4=2a3,
所以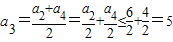 ,
,
即a3的取值范围是(-∞,5].
故答案为:(-∞,5].
点评:本题考查等差数列的性质以及基本运算.在等差数列中,如m+n=p+q,则am+an=ap+aq,要求熟练记住这个性质.
解答:解:在等差数列中由a2≤6,a4≤4得a2+a4=2a3,
所以
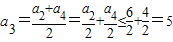 ,
,即a3的取值范围是(-∞,5].
故答案为:(-∞,5].
点评:本题考查等差数列的性质以及基本运算.在等差数列中,如m+n=p+q,则am+an=ap+aq,要求熟练记住这个性质.

练习册系列答案
相关题目