题目内容
函数f（x）=
+
+cx+d（a＜b）在R上单调递增，则
的最小值为（ ）A．1
B．3
C．4
D．9
【答案】分析：利用导数研究函数的单调性、二次函数的单调性即可得出．
解答：解：f′（x）=ax2+bx+c．
∵三次函数f（x）=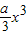
+
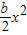+cx+d（a＜b）在R上单调递增，
∴f′（x）≥0在R上恒成立（不恒等于0），
∴
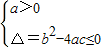，即a＞0，b2≤4ac，
∴
，
∴
=
≥
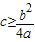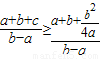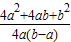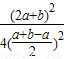，当且仅当a=b-a，即b=2a时取等号，
故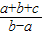
的最小值为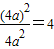 
故答案为 C
点评：熟练掌握导数研究函数的单调性、二次函数的单调性是解题的关键．
解答：解：f′（x）=ax2+bx+c．
∵三次函数f（x）=
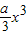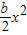++cx+d（a＜b）在R上单调递增，∴f′（x）≥0在R上恒成立（不恒等于0），
∴
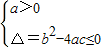，即a＞0，b2≤4ac，∴
，∴
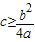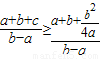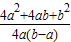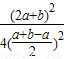=≥，当且仅当a=b-a，即b=2a时取等号，故
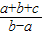的最小值为 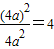故答案为 C
点评：熟练掌握导数研究函数的单调性、二次函数的单调性是解题的关键．
练习册系列答案
相关题目
将函数f（x）=sin（2x-
）的图象左移
，再将图象上各点横坐标压缩到原来的
，则所得到的图象的解析式为（ ）
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| A、y=sinx | ||
B、y=sin（4x+
| ||
C、y=sin（4x-
| ||
D、y=sin（x-
|
设函数f（x）的定义域为D，若存在非零实数l使得对于任意x∈M（M⊆D），有x+l∈D，且f（x+l）≥f（x），则称f（x）为M上的l高调函数．如果定义域为R的函数f（x）是奇函数，当x≥0时，f（x）=|x-a2|-a2，且f（x）为R上的4高调函数，那么实数a的取值范围是（ ）
| A、[-1，1] | B、（-1，1） | C、[-2，2] | D、（-2，2） |
对函数f（x）给出以下性质：①对任意x∈R，f（x+π）=f（x）恒成立；②图象关于直线x=
对称；③在[-
，
]上是增函数．则同时具有以上性质的函数是（ ）
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
A、f(x)=sin(2x+
| ||
B、f(x)=sin(2x-
| ||
C、f(x)=cos(2x+
| ||
D、f(x)=cos(2x-
|