题目内容
四枚不同的金属纪念币A、B、C、D,投掷时,A、B两枚正面向上的概率为分别为 ,另两枚C、D正面向上的概率分别为a(0<a<1).这四枚纪念币同时投掷一次,设ξ表示出现正面向上的枚数.
,另两枚C、D正面向上的概率分别为a(0<a<1).这四枚纪念币同时投掷一次,设ξ表示出现正面向上的枚数.
(1)若A、B出现一正一反与C、D出现两正的概率相等,求a的值;
(2)求ξ的分布列及数学期望(用a表示);
(3)若有2枚纪念币出现正面向上的概率最大,求a的取值范围.
解:(1)设从M中任取一个元素是(3,5)的事件为B,则P(B)= ,
,
所以从M中任取一个元素是(3,5)的概率为 ,
,
(2)设从M中任取一个元素,x+y≥10的事件为C,有
(4,6),(6,4),(5,5),(5,6),(6,5),(6,6)
则P(C)= ,所以从M中任取一个元素x+y≥10的概率为
,所以从M中任取一个元素x+y≥10的概率为 .
.
(3)ξ可能取的值为2,3,4,5,6,7,8,9,10,11,12
P(ξ=2)= ,P(ξ=3)=
,P(ξ=3)=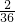 ,P(ξ=4)=
,P(ξ=4)=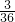 ,P(ξ=5)=
,P(ξ=5)=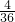 ,P(ξ=6)=
,P(ξ=6)= ,P(ξ=7)=
,P(ξ=7)=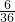 ,
,
P(ξ=8)= ,P(ξ=9)=
,P(ξ=9)=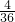 ,P(ξ=10)=
,P(ξ=10)=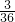 ,P(ξ=11)=
,P(ξ=11)=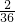 ,P(ξ=12)=
,P(ξ=12)= ,
,
∴ξ的分布列为
∴Eξ=


=7.
分析:(1)设从M中任取一个元素是(3,5)的事件为B,则P(B)= ,由此能求出从M中任取一个元素是(3,5)的概率.
,由此能求出从M中任取一个元素是(3,5)的概率.
(2)设从M中任取一个元素,x+y≥10的事件为C,有(4,6),(6,4),(5,5),(5,6),(6,5),(6,6),由此能求出从M中任取一个元素x+y≥10的概率.
(3)ξ可能取的值为2,3,4,5,6,7,8,9,10,11,12,P(ξ=2)= ,P(ξ=3)=
,P(ξ=3)=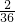 ,P(ξ=4)=
,P(ξ=4)=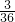 ,P(ξ=5)=
,P(ξ=5)=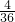 ,P(ξ=6)=
,P(ξ=6)= ,P(ξ=7)=
,P(ξ=7)=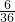 ,P(ξ=8)=
,P(ξ=8)= ,P(ξ=9)=
,P(ξ=9)=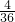 ,P(ξ=10)=
,P(ξ=10)=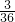 ,P(ξ=11)=
,P(ξ=11)=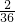 ,P(ξ=12)=
,P(ξ=12)= ,由此能求出ξ的分布列和Eξ.
,由此能求出ξ的分布列和Eξ.
点评:本题考查离散型随机变量的数学期望和方差,综合性强,难度大,易出错.解题时要认真审题,仔细解答.注意理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,体现了化归的重要思想.
 ,
,所以从M中任取一个元素是(3,5)的概率为
 ,
,(2)设从M中任取一个元素,x+y≥10的事件为C,有
(4,6),(6,4),(5,5),(5,6),(6,5),(6,6)
则P(C)=
 ,所以从M中任取一个元素x+y≥10的概率为
,所以从M中任取一个元素x+y≥10的概率为 .
.(3)ξ可能取的值为2,3,4,5,6,7,8,9,10,11,12
P(ξ=2)=
 ,P(ξ=3)=
,P(ξ=3)=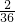 ,P(ξ=4)=
,P(ξ=4)=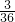 ,P(ξ=5)=
,P(ξ=5)=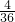 ,P(ξ=6)=
,P(ξ=6)= ,P(ξ=7)=
,P(ξ=7)=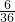 ,
,P(ξ=8)=
 ,P(ξ=9)=
,P(ξ=9)=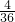 ,P(ξ=10)=
,P(ξ=10)=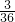 ,P(ξ=11)=
,P(ξ=11)=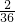 ,P(ξ=12)=
,P(ξ=12)= ,
,∴ξ的分布列为
| ξ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| P |  | 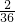 | 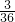 | 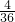 |  | 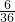 |  | 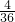 | 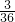 | 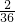 |  |



=7.
分析:(1)设从M中任取一个元素是(3,5)的事件为B,则P(B)=
 ,由此能求出从M中任取一个元素是(3,5)的概率.
,由此能求出从M中任取一个元素是(3,5)的概率.(2)设从M中任取一个元素,x+y≥10的事件为C,有(4,6),(6,4),(5,5),(5,6),(6,5),(6,6),由此能求出从M中任取一个元素x+y≥10的概率.
(3)ξ可能取的值为2,3,4,5,6,7,8,9,10,11,12,P(ξ=2)=
 ,P(ξ=3)=
,P(ξ=3)=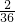 ,P(ξ=4)=
,P(ξ=4)=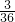 ,P(ξ=5)=
,P(ξ=5)=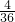 ,P(ξ=6)=
,P(ξ=6)= ,P(ξ=7)=
,P(ξ=7)=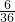 ,P(ξ=8)=
,P(ξ=8)= ,P(ξ=9)=
,P(ξ=9)=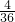 ,P(ξ=10)=
,P(ξ=10)=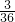 ,P(ξ=11)=
,P(ξ=11)=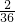 ,P(ξ=12)=
,P(ξ=12)= ,由此能求出ξ的分布列和Eξ.
,由此能求出ξ的分布列和Eξ.点评:本题考查离散型随机变量的数学期望和方差,综合性强,难度大,易出错.解题时要认真审题,仔细解答.注意理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,体现了化归的重要思想.

练习册系列答案
相关题目
 ,另两枚C、D正面向上的概率分别为a(0<a<1).这四枚纪念币同时投掷一次,设ξ表示出现正面向上的枚数.
,另两枚C、D正面向上的概率分别为a(0<a<1).这四枚纪念币同时投掷一次,设ξ表示出现正面向上的枚数. ,另两枚C,D(质地不均匀)正面向上的概率均为a(0<a<1).将这四枚纪念币同时投掷一次,设ξ表示出现正面向上的枚数.
,另两枚C,D(质地不均匀)正面向上的概率均为a(0<a<1).将这四枚纪念币同时投掷一次,设ξ表示出现正面向上的枚数.