Question

【题目】已知，，.

（1）解关于的方程；

（2）设，时，对任意，总有成立，求的取值范围.

Answer 1

【答案】（1）见解析；（2）.

【解析】

（1）利用换元法得到含参数的一元二次方程，再对分类讨论，分析方程解的情况；

（2）题中任意，总有可以看作区间内函数最大值与函数最小值的差值问题，然后对参数进行分类讨论，确定函数在区间上的单调性，从而确定函数在区间上的最值，再根据不等式求出参数的取值范围.

（1）由题知，

代入有，

整理得，

令，，

即，，

当时，方程无解，

当时，方程有一个解，解得，

当时，方程有两个解，

，

，

当时，方程仅有一个根，

；

（2），代入，

有，

令，，设，

①当时，易知函数在区间单调递增，

又因为，

即，

解得，舍去，

②当时，函数在处取最小值，

当时，，

即函数在区间单调递增，

又因为，

即，

解得，

所以，

当时，，

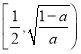即函数在区间单调递减，

在区间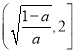单调递增，

又因为，

即，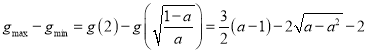

因为当时，恒成立，

所以，

综上.