题目内容
(本小题满分14分)
已知向量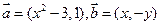 ,(其中实数
,(其中实数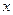 和
和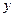 不同时为零),当
不同时为零),当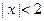 时,有
时,有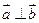 ,当
,当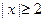 时,
时,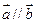 .
.
(1)求函数式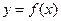 ;
;
(2)求函数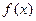 的单调递减区间;
的单调递减区间;
(3)若对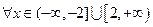 ,都有
,都有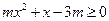 ,求实数
,求实数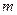 的取值范围.
的取值范围.
已知向量
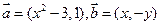 ,(其中实数
,(其中实数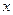 和
和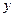 不同时为零),当
不同时为零),当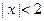 时,有
时,有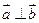 ,当
,当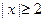 时,
时,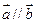 .
.(1)求函数式
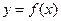 ;
;(2)求函数
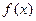 的单调递减区间;
的单调递减区间;(3)若对
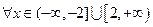 ,都有
,都有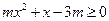 ,求实数
,求实数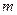 的取值范围.
的取值范围.解:(1)当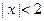 时,由
时,由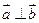 得
得 ,
,
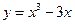 ;(
;(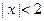 且
且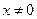 )----------------------------------------------------2分
)----------------------------------------------------2分
当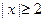 时,由
时,由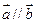 .
.
得 --------------------------------------------------------------4分
--------------------------------------------------------------4分
∴ -----------------------------------5分
-----------------------------------5分
(2)当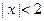 且
且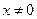 时,
时,
由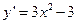 <0,解得
<0,解得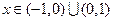 ,-------------------------------------------6分
,-------------------------------------------6分
当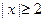 时,
时, ----------------------------8分
----------------------------8分
∴函数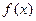 的单调减区间为(-1,0)和(0,1) ------------------------------9分
的单调减区间为(-1,0)和(0,1) ------------------------------9分
(3)对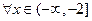
 ,
,
都有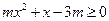 即
即 ,
,
也就是
对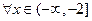
 恒成立,----------------------------------------------------11分
恒成立,----------------------------------------------------11分
由(2)知当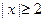 时,
时,
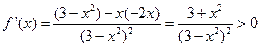
∴函数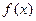 在
在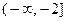 和
和 都单调递增-------------------------------12分
都单调递增-------------------------------12分
又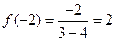 ,
,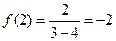
当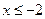 时
时  ,
,
∴当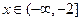 时,
时,  同理可得,当
同理可得,当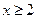 时, 有
时, 有 ,
,
综上所述得,对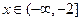
 ,
,
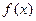 取得最大值2;∴实数
取得最大值2;∴实数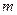 的取值范围为
的取值范围为 . ----------------14分
. ----------------14分
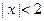 时,由
时,由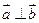 得
得 ,
,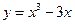 ;(
;(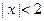 且
且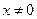 )----------------------------------------------------2分
)----------------------------------------------------2分当
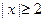 时,由
时,由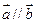 .
.得
 --------------------------------------------------------------4分
--------------------------------------------------------------4分∴
 -----------------------------------5分
-----------------------------------5分(2)当
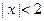 且
且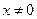 时,
时, 由
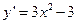 <0,解得
<0,解得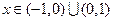 ,-------------------------------------------6分
,-------------------------------------------6分当
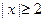 时,
时, ----------------------------8分
----------------------------8分∴函数
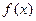 的单调减区间为(-1,0)和(0,1) ------------------------------9分
的单调减区间为(-1,0)和(0,1) ------------------------------9分(3)对
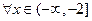
 ,
,都有
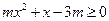 即
即 ,
,也就是

对
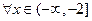
 恒成立,----------------------------------------------------11分
恒成立,----------------------------------------------------11分由(2)知当
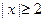 时,
时,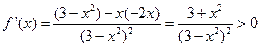
∴函数
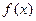 在
在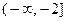 和
和 都单调递增-------------------------------12分
都单调递增-------------------------------12分又
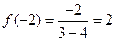 ,
,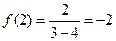
当
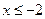 时
时  ,
,∴当
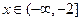 时,
时,  同理可得,当
同理可得,当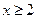 时, 有
时, 有 ,
,综上所述得,对
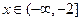
 ,
,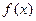 取得最大值2;∴实数
取得最大值2;∴实数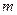 的取值范围为
的取值范围为 . ----------------14分
. ----------------14分略

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 中,角
中,角 所对的边分别为
所对的边分别为 .向量
.向量 ,
, .已知
.已知 ,
, .
. 的大小;
的大小; 若
若 ∥
∥ ,则实数
,则实数 的值是
的值是



 ,则
,则 ( )
( )


 且
且 //
// ,则锐角
,则锐角 的大小为 ( )
的大小为 ( )



 和过原点的直线
和过原点的直线 的交点为
的交点为 、
、 ,则
,则 的值为
的值为  ,
, ,
, ,M是BC的中点,则
,M是BC的中点,则 ____________.(用
____________.(用 、
、 表示)
表示)
 ,则
,则 ____________
____________