题目内容
6. 设函数f(x)在定义域内可导且其图象如图①所示,则导函数y=f′(x)的图象最有可能是( )
设函数f(x)在定义域内可导且其图象如图①所示,则导函数y=f′(x)的图象最有可能是( )| A. | 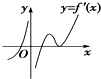 | B. |  | C. |  | D. |  |
分析 根据函数f(x)的图象判断f(x)单调性:x<0时为增函数,对应的f′(x)>0;x>0时,增减变化是增减增,所以对应的f′(x)的符号为大于0,小于0,大于0,所以选出满足以上导数f′(x)的符号的图象即可.
解答 解:根据f(x)图象可以看出:x<0时,f(x)是增函数;
x>0时的单调性是:先增,再减,最后增;
∴对应的f′(x)的符号为:x<0时,f′(x)≥0;
x>0时,f′(x)符号的变化过程为:大于0,小于0,再大于0;
所以符合这样的导数符号的图象为D.
故选:D.
点评 考查观察图象判断函数的单调性,函数单调性和函数导数符号的关系.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
7.已知a>0,b>0,直线3x-4y=0是双曲线S:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1的一条渐近线,双曲线S的离心率为e,则$\frac{3e+{a}^{2}}{b}$的最小值为( )
| A. | $\frac{3\sqrt{5}}{2}$ | B. | $\frac{7\sqrt{5}}{2}$ | C. | $\frac{11\sqrt{5}}{3}$ | D. | $\frac{4\sqrt{15}}{3}$ |
4.使y=cosωx(ω>0)在区间[0,1]上至少出现2次最大值,至多出现3次最大值,则周期T的取值范围是( )
| A. | 1<T≤2 | B. | 1≤T≤2 | C. | $\frac{1}{2}$<T≤1 | D. | $\frac{1}{2}$≤T≤1 |
15.不同字母表示不同的数字,关于下面四进制的加法运算,描述正确的有( )


| A. | 字母A的值是2 | B. | 字母B的值是3 | C. | 字母C的值是2 | D. | 字母D的值是0 |
 如图,已知动圆M过定点F(1,0)且与y轴相切,点F关于圆心M的对称点为F′,点F′的轨迹为H.
如图,已知动圆M过定点F(1,0)且与y轴相切,点F关于圆心M的对称点为F′,点F′的轨迹为H.