题目内容
双曲线与椭圆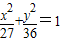 有相同焦点,且经过点
有相同焦点,且经过点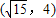 ,求其方程.
,求其方程.
【答案】分析:根据已知中双曲线与椭圆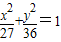 有相同焦点,我们可以设出双曲线的标准方程(含参数a),然后根据经过点
有相同焦点,我们可以设出双曲线的标准方程(含参数a),然后根据经过点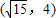 ,得到一个关于a的方程,解方程,即可得到a2的值,进而得到双曲线的方程.
,得到一个关于a的方程,解方程,即可得到a2的值,进而得到双曲线的方程.
解答:解:椭圆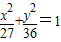 的焦点为(0,±3),即c=3,
的焦点为(0,±3),即c=3,
设双曲线方程为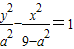
过点(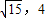 ),则
),则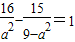 ,
,
得a2=4或a2=36,而a2<9,
∴a2=4,双曲线方程为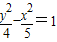
点评:本题考查的知识点是双曲线的标准方程,其中根据已知条件设出双曲线的标准方程(含参数a),并构造一个关于a的方程,是解答本题的关键.
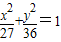 有相同焦点,我们可以设出双曲线的标准方程(含参数a),然后根据经过点
有相同焦点,我们可以设出双曲线的标准方程(含参数a),然后根据经过点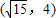 ,得到一个关于a的方程,解方程,即可得到a2的值,进而得到双曲线的方程.
,得到一个关于a的方程,解方程,即可得到a2的值,进而得到双曲线的方程.解答:解:椭圆
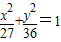 的焦点为(0,±3),即c=3,
的焦点为(0,±3),即c=3,设双曲线方程为
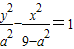
过点(
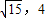 ),则
),则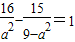 ,
,得a2=4或a2=36,而a2<9,
∴a2=4,双曲线方程为
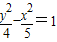
点评:本题考查的知识点是双曲线的标准方程,其中根据已知条件设出双曲线的标准方程(含参数a),并构造一个关于a的方程,是解答本题的关键.

练习册系列答案
相关题目
 有相同焦点,且经过点
有相同焦点,且经过点 ,
, 有相同焦点,且经过点
有相同焦点,且经过点 ,求双曲线的方程、
,求双曲线的方程、 有相同焦点,且经过点
有相同焦点,且经过点 ,求双曲线的方程
,求双曲线的方程  有相同焦点,且经过点
有相同焦点,且经过点 .
. 作斜率为1的直线交双曲线于
作斜率为1的直线交双曲线于 两点,求
两点,求 .
.