题目内容
（2013•海口二模）已知球O的半径OD=3，线段OD上一点M满足OM=2MD，过M且与OD成30°角的平面截球O的表面得到圆N，三棱锥S-ABC的底面ABC内接于圆N，顶点S在球O的表面上，则三棱锥S-ABC体积的最大值为（ ）
分析：根据题意，算出OM=2且MD=1．连结ON，小圆中作出过MN的半径NK，连结KO．由圆N所在平面与直线OD成30°角算出ON=1，从而得到三棱锥S-ABC高的最大值为NS=ON+OS=4．再由圆的截面圆性质算出圆N的半径r=2
，从而得到△ABC的面积最大值为S=6
，由此结合锥体体积公式即可算出三棱锥S-ABC体积的最大值．
| 2 |
| 3 |
解答：解：∵OD=3，且OM=2MD，∴OM=2，MD=1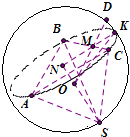
连结ON，小圆中作出过MN的半径NK，连结KO
∵圆N所在平面与OD成30°角
∴Rt△OMN中，ON=OMsin30°=1
∵三棱锥S-ABC的底面△ABC在圆N所在的平面内
∴当点S在直线ON上，且在NO的延长线上时，三棱锥S-ABC的高等于NS=4，
此时三棱锥S-ABC的高达到最大值
∵Rt△KON中，OK=OD=3，ON=1，∴圆N的半径r=NK=
=2
∵圆的内接等边三角形面积是其内接三角形的面积最大值
∴△ABC的面积最大值为S=2r2sinAsinBsinC=2×8×（
）3=6
由此可得三棱锥S-ABC体积的最大值为V=
S△ABC×NS=
×6
×4=8
故选：B
连结ON，小圆中作出过MN的半径NK，连结KO
∵圆N所在平面与OD成30°角
∴Rt△OMN中，ON=OMsin30°=1
∵三棱锥S-ABC的底面△ABC在圆N所在的平面内
∴当点S在直线ON上，且在NO的延长线上时，三棱锥S-ABC的高等于NS=4，
此时三棱锥S-ABC的高达到最大值
∵Rt△KON中，OK=OD=3，ON=1，∴圆N的半径r=NK=
| 32-12 |
| 2 |
∵圆的内接等边三角形面积是其内接三角形的面积最大值
∴△ABC的面积最大值为S=2r2sinAsinBsinC=2×8×（
| ||
| 2 |
| 3 |
由此可得三棱锥S-ABC体积的最大值为V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
故选：B
点评：本题在球O中给出与半径OD成30度角的截面，求三棱锥S-ABC体积的最大值．着重考查了球的截面圆性质、直线与平面所成角、圆内接三角形面积求法和锥体体积公式等知识，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
（2013•海口二模）已知集合M={-1，0，1}，N={0，1，2}，则如图所示韦恩图中的阴影部分所表示的集合为（ ）
（2013•海口二模）设偶函数f（x）=Asin（ωx+?）（A＞0，ω＞0，0＜?＜π）的部分图象如图所示，△KLM为等腰直角三角形，∠KML=90°，KL=1，则