题目内容
(理)C1:![]() (a>b>0)左右焦点分别为F1,F2,右顶点为A,P为C1上任意一点,
(a>b>0)左右焦点分别为F1,F2,右顶点为A,P为C1上任意一点,![]() 的最大值的取值范围为[c2,3c2],c=
的最大值的取值范围为[c2,3c2],c=![]()
(1)求点C1的离心率e的范围;
(2)设双曲线C2以C1的焦点为顶点,顶点为焦点,B是双曲线C2在第一象限上任意一点,当e取最小值时,猜想是否存在常数λ(λ>0),使∠BAF1=λ∠BF1A恒成立?若存在,求出λ的值;若不存在,说明理由.
答案:
解析:
解析:
|
(理)(1)P(x,y), (2)e=1/2,C2:3x2-y2=3c2,A(2c,0),B(x0,y0)(x0,y0>0),AB⊥x轴时,λ=2,猜想λ=2;x0≠2c时 tan∠BAF1=- |

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
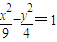 ,伸缩比λ=2,求C1关于原点“伸缩变换”后所得曲线C2的方程;
,伸缩比λ=2,求C1关于原点“伸缩变换”后所得曲线C2的方程;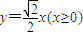 ,如果椭圆C1:
,如果椭圆C1: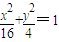 经“伸缩变换”后得到椭圆C2,若射线l与椭圆C1、C2分别交于两点A、B,且
经“伸缩变换”后得到椭圆C2,若射线l与椭圆C1、C2分别交于两点A、B,且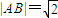 ,求椭圆C2的方程;
,求椭圆C2的方程;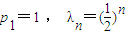 ,求数列{pn}的通项公式pn.
,求数列{pn}的通项公式pn.