Question

过双曲线

x2

a2

-

y2

b2

=1(a＞0，b＞0)的左焦点F作圆x²+y²=a²的两条切线，切点分别为A、B，双曲线左顶点为M，若∠AMB=120°，则该双曲线的离心率为（　　）

• A、

  2

• B、

  3

• C、3
• D、2

Answer 1

分析：依题意，作出图形，易求该双曲线的离心率e=

c

a

=

OF

OA

=2，从而得到答案．

解答：解：依题意，作图如下：

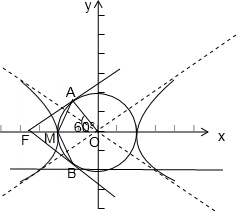
∵OA⊥FA，∠AMO=60°，OM=OA，
∴△AMO为等边三角形，
∴OA=OM=a，
在直角三角形OAF中，OF=c，
∴该双曲线的离心率e=

c

a

=

OF

OA

=

1

sin30°

=2，
故选：D．

点评：本题考查双曲线的简单性质，考查作图能力与解三角形的能力，属于中档题．