题目内容
已知数列{an}中,a1=1,当n≥2时, .
.
(Ⅰ)证明数列{Sn}是一个等差数列;
(Ⅱ)求an.
(1)证明:当n=1时,S1=a1=1 (2分)
当 n≥2时an=Sn-Sn-1=(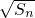 +
+ )(
)( 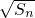 -
- )=
)=
而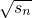 +
+ ≠0
≠0
∴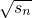 -
- =
= (4分)
(4分)
∴数列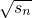 是一个等差数列 (6分)
是一个等差数列 (6分)
(2)由(1)得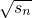 =
= Sn=(
Sn=(  )2
)2
当n=1时 a1=S1当n>1时(10分)
an=Sn-Sn-1=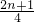
∴an= (12分)
(12分)
分析:(1)由n=1时,可得S1=a1=1,n≥2时,利用an=Sn-Sn-1=(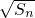 +
+ )(
)( 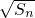 -
- )=
)= 可证得
可证得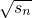 -
- =
= ,即可证明
,即可证明
(2)由(1)可求Sn=( )2,利用n=1时 a1=S1,n>1时an=Sn-Sn-1可求
)2,利用n=1时 a1=S1,n>1时an=Sn-Sn-1可求
点评:本题主要考查了等差数列的定义在证明中的应用,数列的递推公式an= 的应用是实现数列的和与项转化的关键
的应用是实现数列的和与项转化的关键
当 n≥2时an=Sn-Sn-1=(
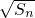 +
+ )(
)( 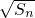 -
- )=
)=
而
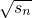 +
+ ≠0
≠0∴
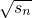 -
- =
= (4分)
(4分)∴数列
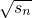 是一个等差数列 (6分)
是一个等差数列 (6分)(2)由(1)得
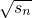 =
= Sn=(
Sn=(  )2
)2当n=1时 a1=S1当n>1时(10分)
an=Sn-Sn-1=
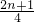
∴an=
 (12分)
(12分)分析:(1)由n=1时,可得S1=a1=1,n≥2时,利用an=Sn-Sn-1=(
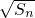 +
+ )(
)( 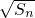 -
- )=
)= 可证得
可证得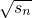 -
- =
= ,即可证明
,即可证明(2)由(1)可求Sn=(
 )2,利用n=1时 a1=S1,n>1时an=Sn-Sn-1可求
)2,利用n=1时 a1=S1,n>1时an=Sn-Sn-1可求点评:本题主要考查了等差数列的定义在证明中的应用,数列的递推公式an=
 的应用是实现数列的和与项转化的关键
的应用是实现数列的和与项转化的关键 
练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|