题目内容
(1)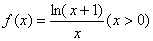 ,求证:若
,求证:若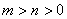 ,则
,则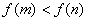 .
.
(2)求 在[1,2]上的最大最小值。
在[1,2]上的最大最小值。
解:(1)方法一:设B(m,ln(m+1)),A(n,ln(n+1))为函数y=ln(x+1)图象上两点
而f(m),f(n)分别B、A两点与原点连线的斜率,
显然kOA>kOB
即f(m)<f(n) ……………5分
方法二: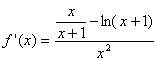
令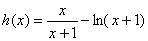
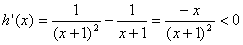
∴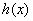 是减函数
是减函数
由x>0得,h(x)<h(0)=0
∴
∴f(x)是减函数
由m>n>0可得f(m)<f(n) ……………5分
(2)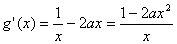
令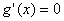 得2ax2=1 ……………①
得2ax2=1 ……………①
当a≤0时,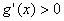 ,
,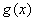 在[1,2]上为增函数
在[1,2]上为增函数
∴最大值为g(2),最小值为g(1)]
当a>0时,由①得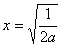
若 ≥2即0<a≤
≥2即0<a≤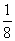 时,
时, ≥0,
≥0,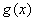 在[1,2]上为增函数
在[1,2]上为增函数
∴最大值为g(2),最小值为g(1)
若 ≤1即a≥
≤1即a≥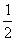 时,
时, ≤0,
≤0,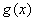 在[1,2]上为减函数
在[1,2]上为减函数
∴最大值为g(1),最小值为g(2)
若1< <2即
<2即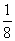 <a<
<a<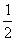 时
时
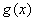 在(1,
在(1, )上为增函数,在(
)上为增函数,在( ,2)上为减函数
,2)上为减函数
∴最大值为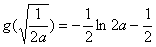
最小值为g(2),g(1)中的较小的数
∵g(2)-g(1)=ln2-3a
若a≤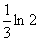 ,则g(2)≥g(1)
,则g(2)≥g(1)
若a>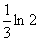 ,则g(2)<g(1)
,则g(2)<g(1)
∴当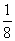 <a≤
<a≤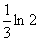 时,最小值为g(1)
时,最小值为g(1)
当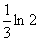 <a<
<a<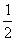 时,最小值为g(2)
时,最小值为g(2)
综上得:a≤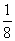 时,最大值为ln2-4a,最小值为-a
时,最大值为ln2-4a,最小值为-a
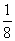 <a≤
<a≤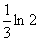 时,最大值为
时,最大值为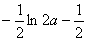 ,最小值为-a
,最小值为-a
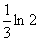 <a<
<a<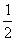 时,最大值为
时,最大值为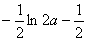 ,最小值为ln-4a
,最小值为ln-4a
a≥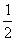 时,最大值为-a,最小值为ln2-4a. ……………13分
时,最大值为-a,最小值为ln2-4a. ……………13分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的一条渐近线的倾斜角为
的一条渐近线的倾斜角为 ,则
,则 .
. ,G,
,G, 成等比数列. 且
成等比数列. 且 >0,则
>0,则 .
. 为增函数的区间是
为增函数的区间是







 的内角
的内角 的对边长分别为
的对边长分别为 ,若
,若 ,且
,且 ,则
,则 __________
__________ B.m<0
B.m<0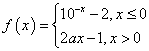 (
( 是常数且
是常数且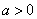 ).给出下列命题:
).给出下列命题: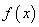 的最小值是
的最小值是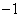 ;
;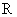 上是单调函数;
上是单调函数;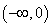 上的零点是
上的零点是 ;
;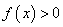 在
在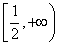 上恒成立,则
上恒成立,则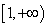 ;
;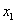 ,
,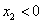 且
且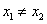 ,恒有
,恒有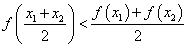 .
.