题目内容
a,b,c∈R+且互不相等,求证:a4+b4+c4≥a2b2+b2c2+c2a2.
证明: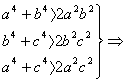 a4+b4+b4+c4+a4+c4>2a2b2+2b2c2+2a2c2
a4+b4+b4+c4+a4+c4>2a2b2+2b2c2+2a2c2![]() a4+b4+c4>a2b2+b2c2+c2a2.
a4+b4+c4>a2b2+b2c2+c2a2.
温馨提示
证明对称不等式(如例3),通常都是通过几个平均值不等式相加(或减)得出目标不等式.

练习册系列答案
相关题目
题目内容
a,b,c∈R+且互不相等,求证:a4+b4+c4≥a2b2+b2c2+c2a2.
证明: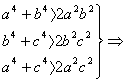 a4+b4+b4+c4+a4+c4>2a2b2+2b2c2+2a2c2
a4+b4+b4+c4+a4+c4>2a2b2+2b2c2+2a2c2![]() a4+b4+c4>a2b2+b2c2+c2a2.
a4+b4+c4>a2b2+b2c2+c2a2.
温馨提示
证明对称不等式(如例3),通常都是通过几个平均值不等式相加(或减)得出目标不等式.
