题目内容

将边长为1 m的正三角形薄铁皮沿一条平行于某边的直线剪成两块,其中一块是梯形,记s=,则s的最小值是　　　　. 
如图所示,设梯形上底边长为x(0<x<1),
则梯形两腰长为1-x,高为 (1-x).

s=
=
=-·.
令u(x)=,0<x<1.
∵u′(x)=
=,
∴当0<x<时,u′(x)>0,u(x)单调递增;
当<x<1时,u′(x)<0,u(x)单调递减,
∴当x=时,u(x)最大,s最小,
smin=-×
=
=.
练习册系列答案
相关题目
已知函数f(x)＝x2－4，设曲线y＝f(x)在点(xn，f(xn))
处的切线与x轴的交点为(xn＋1,0)(n∈N＋)，其中x1为正实数．
(1)用xn表示xn＋1；
(2)求证：对一切正整数n，xn＋1≤xn的充要条件是x1≥2；
(3)若x1＝4，记an＝lg ，证明数列{an}成等比数列，并求数列{xn}的通项公式．
设P(x，y)为函数y＝x2－1(x＞)图象上一动点，记m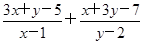＝，则当m最小时，点P的坐标为________．
已知函数f(x)＝，x∈[－1，8]，函数g(x)＝ax＋2，x∈[－1，8]，若存在x∈[－1，8]，使f(x)＝g(x)成立，则实数a的取值范围是________．
在实数的原有运算法则中,我们补充定义新运算“⊕”;当a≥b时,a⊕b=a;当a<b时,a⊕b=b2,函数f(x)=(1⊕x)·x(其中“·”仍为通常的乘法),则函数f(x)在[0,2]上的值域为(　　)
A．[0,4]B．[1,4]C．[0,8]D．[1,8]
设函数f(x)=x3cosx+1.若f(a)=11,则f(-a)=　　　. 
已知函数f(x)＝x2＋ax＋b(a，b∈R)的值域为[0，＋∞)，若关于x的不等式f(x)＜c的解集为(m，m＋6)，则实数c的值为________．
若对于定义在R上的函数f(x)，其图象是连续不断的，且存在常数λ(λ∈R)使得f(x＋λ)＋λf(x)＝0对任意实数都成立，则称f(x)是一个“λ伴随函数”．下列关于“λ伴随函数”的结论：①f(x)＝0不是常数函数中唯一一个“λ伴随函数”；②f(x)＝x不是“λ伴随函数”；③f(x)＝x2是“λ伴随函数”；④“伴随函数”至少有一个零点．其中正确的结论个数是(  )
A．1 B．2C．3 D．4
已知符号函数sgn(x)=则函数f(x)=sgn(lnx)-lnx的零点个数为(　　)
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网