题目内容
函数f(x)的定义域为D,若满足①f(x)在D内是单调函数,②存在[a,b]⊆D,使f(x)在[a,b]上的值域为[-b,-a],那么y=f(x)叫做对称函数,现有f(x)=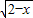 -k是对称函数,那么k的取值范围是 .
-k是对称函数,那么k的取值范围是 .
【答案】分析:函数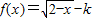 在定义域(-∞,2]上是减函数,由②可得 f(a)=-a,f(b)=-b,由此推出 a和 b 是方程
在定义域(-∞,2]上是减函数,由②可得 f(a)=-a,f(b)=-b,由此推出 a和 b 是方程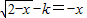 在(-∞,2]上的两个根.利用换元法,转化为∴k=-t2+t+2=-(t-
在(-∞,2]上的两个根.利用换元法,转化为∴k=-t2+t+2=-(t- )2+
)2+ 在[0,+∞)有两个不同实根,解此不等式求得 k 的范围即为所求.
在[0,+∞)有两个不同实根,解此不等式求得 k 的范围即为所求.
解答:解:由于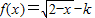 在(-∞,2]上是减函数,故满足①,
在(-∞,2]上是减函数,故满足①,
又f(x)在[a,b]上的值域为[-b,-a],
∴所以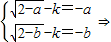 a和 b 是关于x的方程
a和 b 是关于x的方程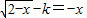 在(-∞,2]上有两个不同实根.
在(-∞,2]上有两个不同实根.
令t=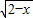 ,则x=2-t2,t≥0,
,则x=2-t2,t≥0,
∴k=-t2+t+2=-(t- )2+
)2+ ,
,
∴k的取值范围是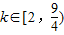 ,
,
故答案为: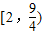 .
.
点评:本题考查函数的单调性的应用,求函数的值域,体现了转化的数学思想,得到a和 b 是方程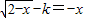 在(-∞,2]上的两个根,是解题的难点,属中档题.
在(-∞,2]上的两个根,是解题的难点,属中档题.
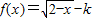 在定义域(-∞,2]上是减函数,由②可得 f(a)=-a,f(b)=-b,由此推出 a和 b 是方程
在定义域(-∞,2]上是减函数,由②可得 f(a)=-a,f(b)=-b,由此推出 a和 b 是方程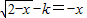 在(-∞,2]上的两个根.利用换元法,转化为∴k=-t2+t+2=-(t-
在(-∞,2]上的两个根.利用换元法,转化为∴k=-t2+t+2=-(t- )2+
)2+ 在[0,+∞)有两个不同实根,解此不等式求得 k 的范围即为所求.
在[0,+∞)有两个不同实根,解此不等式求得 k 的范围即为所求.解答:解:由于
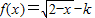 在(-∞,2]上是减函数,故满足①,
在(-∞,2]上是减函数,故满足①,又f(x)在[a,b]上的值域为[-b,-a],
∴所以
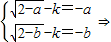 a和 b 是关于x的方程
a和 b 是关于x的方程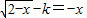 在(-∞,2]上有两个不同实根.
在(-∞,2]上有两个不同实根.令t=
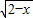 ,则x=2-t2,t≥0,
,则x=2-t2,t≥0,∴k=-t2+t+2=-(t-
 )2+
)2+ ,
,∴k的取值范围是
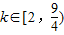 ,
,故答案为:
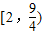 .
.点评:本题考查函数的单调性的应用,求函数的值域,体现了转化的数学思想,得到a和 b 是方程
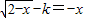 在(-∞,2]上的两个根,是解题的难点,属中档题.
在(-∞,2]上的两个根,是解题的难点,属中档题. 
练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
若函数f(x)的定义域为[-1,2],则函数
的定义域为( )
| f(x+2) |
| x |
| A、[-1,0)∪(0,2] |
| B、[-3,0) |
| C、[1,4] |
| D、(0,2] |