题目内容
2.在△ABC中,a,b,c分别是角 A,B,C的对边,且bcosC+ccosB=2acosB.(Ⅰ)求角B的大小;
(Ⅱ)若函数f(x)=sin(2x+B)+sin(2x-B)+2cos2x-1,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间$[{-\frac{π}{4},\frac{π}{4}}]$上的最大值和最小值.
分析 (Ⅰ)由三角函数恒等变换的应用化简已知等式可得sinA=2sinAcosB,又sinA≠0,可得$cosB=\frac{1}{2}$.从而可求B.
(Ⅱ)由(Ⅰ)知$B=\frac{π}{3}$,化简函数解析式可得f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),利用周期公式可求f(x)的最小正周期,由$x∈[-\frac{π}{4},\frac{π}{4}]$,利用正弦函数的图象和性质可求$sin(2x+\frac{π}{4})∈[-\frac{{\sqrt{2}}}{2},1]$,从而得解.
解答 (本题满分为12分)
解:(Ⅰ)由∵bcosC+ccosB=2acosB,
变为sinBcosC+sinCcosB=2sinAcosB,
即sinA=2sinAcosB.
∴$cosB=\frac{1}{2}$.∴$B=\frac{π}{3}$
(Ⅱ)由(Ⅰ)知$B=\frac{π}{3}$,
所以$f(x)=sin(2x+\frac{π}{3})+sin(2x-\frac{π}{3})+2co{s^2}x-1$=$sin2xcos\frac{π}{3}+cos2xsin\frac{π}{3}+sin2xcos\frac{π}{3}-cos2xsin\frac{π}{3}+cos2x$=$sin2x+cos2x=\sqrt{2}sin(2x+\frac{π}{4})$…(7分)
(1)f(x)的最小正周期$T=\frac{2π}{2}=π$.…(8分)
(2)∵$x∈[-\frac{π}{4},\frac{π}{4}]$,∴$2x∈[-\frac{π}{2},\frac{π}{2}],2x+\frac{π}{4}∈[-\frac{π}{4},\frac{3π}{4}]$,$sin(2x+\frac{π}{4})∈[-\frac{{\sqrt{2}}}{2},1]$
所以,$f(x)=\sqrt{2}sin(2x+\frac{π}{4})∈[-1,\sqrt{2}]$…(10分)
故$f{(x)_{max}}=\sqrt{2},f{(x)_{min}}=-1$.…(12分)
点评 本题主要考查了正弦定理、三角函数恒等变换的应用,考查了正弦函数的图象和性质,属于基本知识的考查.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
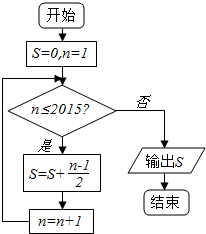
| A. | $\frac{2015×2016}{4}$ | B. | $\frac{2014×2015}{4}$ | C. | $\frac{2015×2016}{2}$ | D. | $\frac{2014×2015}{2}$ |