题目内容
已知数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ,(n=1,2,3…)数列
,(n=1,2,3…)数列![]() 中,
中,![]() ,点
,点![]() 在直线
在直线![]() 上。
上。
(Ⅰ)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(Ⅱ)记![]() ,求满足
,求满足![]() 的最大正整数n。
的最大正整数n。
解:(I)∵ ![]()
∴ 当![]() 时,
时,![]()
即![]() ∵
∵ ![]() ∴
∴ ![]()
![]()
即数列![]() 是等比数列.
是等比数列.
∵ ![]() ∴
∴ ![]() 即
即![]()
∴ ![]() …………………3分
…………………3分
∵ 点![]() 在直线
在直线![]() 上
上
∴ ![]() ∴
∴ ![]()
即数列![]() 是等差数列,又
是等差数列,又![]() ∴
∴ ![]() …………………6分
…………………6分
(II)![]()
![]() ①(7分)
①(7分)
∴ ![]() ②
②
①-②得![]()
即![]() …………………9分
…………………9分
∴ ![]() (10分)
(10分)
∵ ![]() 即
即![]()
于是![]() (11分)
(11分)
又由于当![]() 时,
时,![]() (12分)
(12分)
当![]() 时,
时,![]() (13分)
(13分)
故满足条件![]() 最大的正整数n为4(14分) …………………12分
最大的正整数n为4(14分) …………………12分

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 求使不等式
求使不等式 的前n项和为
的前n项和为 ,
, 且满足
且满足 +n (n>1且n∈
+n (n>1且n∈ )
) ,求使得不等式
,求使得不等式 成立的最小正整数n的值
成立的最小正整数n的值  的前n项和为
的前n项和为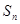 ,且
,且 ,
, ,并猜想
,并猜想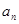 的表达式。
的表达式。