Question

【题目】已知A为焦距为的椭圆E：（a＞b＞0）的右顶点，点P（0，），直线PA交椭圆E于点B，．

（1）求椭圆E的方程；

（2）设过点P且斜率为的直线与椭圆E交于M、N两点（M在P、N之间），若四边形MNAB的面积是△PMB面积的5倍．求直线的斜率．

Answer 1

【答案】（1）+=1；（2）k=±

【解析】

（1）先根据条件得B点坐标，代入椭圆方程，再与焦距联立方程组解得（2）根据面积关系得，联立直线方程与椭圆方程，利用韦达定理建立等量关系解得斜率.

（1）由题意，得焦距2c=2，∴2c=2，c=，

∵，所以点B为线段AP的中点，

因为点P（0，2），A（a，0），

∴B（，），

因为点B（，）在椭圆E上，∴+=1，

即b2=4，2=b2+c2=9，

∴椭圆E的方程为+=1．

（2）由题可得S△PAN=6S△PBM，即|PA||PN|sin∠APN=6×|PB||PM|sin∠BPM，

∴|PN|=3||，∴，设M（x1，y1），N（x2，y2），

于是=（x1，y1-2），=（x2，y2-2），

∴3（x1，y1-2）=（x2，y2-2），

∴x2=3 x1，即=3，于是+=，即=，①，

联立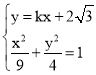，消去y，整理得（9k2+4）x2+36kx+72=0，

由△=（36k）2-4×（9k2+4）×72＞0，解得k2＞，

∴x1+x2=-，x1x2=，

代入①可解得k2=，满足k2＞，∴k=±，即直线l的斜率k=±．