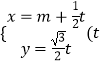Question

【题目】如图，在四棱台ABCD﹣A1B1C1D1中，底面ABCD为平行四边形，∠BAD=120°，M为CD上的点．且∠A1AB=∠A1AD=90°，AD=A1A=2，A1B1=DM=1．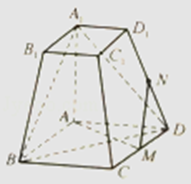
（1）求证：AM⊥A1B；
（2）若M为CD的中点，N为棱DD1上的点，且MN与平面A1BD所成角的正弦值为 ，试求DN的长．

Answer 1

【答案】
（1）证明：在平行四边形ABCD中，∠BAD=120°，∴∠ADM=60°，

在△ADM中，AD=2，DM=1，∴ = ，

可得AD2=AM2+DM2，∴AM⊥CD．

又CD∥AB，∴AM⊥AB，

∵∠A1AB=∠A1AD=90°，∴A1A⊥AB，A1A⊥AD．

又∵AB∩AD=A，AB，AD平面ABCD，

∴AA1⊥ABCD，又AM平面ABCD，

∴AM⊥AA1．又∵AB∩AA1=A，AB，AA1平面AA1B1B，

∴AM⊥平面AA1B1B．又∵A1B平面AA1B1B，

∴AM⊥A1B

（2）解：∵M为CD的中点，DM=1，∴CD=2，

所以四边形ABCD为菱形．

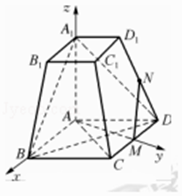
分别以AB，AM，AA1为x轴，y轴，z轴，建立如图所示的空间直角坐标系A﹣xyz，

则点 ．

∴ ．

设平面A1BD的一个法向量为 ，则有 ，

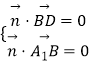∴ ，令x=1，则 ，

设 ，∴ ，

∴ ，

∴ ，∴2λ2﹣13λ+6=0，

∴ 或λ=6（舍去）．

∴ ．

【解析】（1）利用勾股定理逆定理得出AM⊥CD，即AM⊥AB，结合AM⊥AA1得出AM⊥平面AA1B1B，于是AM⊥A1B；（2）建立空间坐标系，根据MN与平面A1BD所成角的大小确定N点位置，从而得出DN的长．
【考点精析】本题主要考查了直线与平面垂直的性质的相关知识点，需要掌握垂直于同一个平面的两条直线平行才能正确解答此题．