题目内容
![]() 点
点![]() 在直线
在直线![]() 上,若存在过
上,若存在过![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,且
两点,且![]() ,则称点
,则称点![]() 为“ 点”,那么下列结论中正确的是 ( )
为“ 点”,那么下列结论中正确的是 ( )
A.直线![]() 上的所有点都是“
上的所有点都是“![]() 点”
点”
![]() B.直线
B.直线![]() 上仅有有限个点是“
上仅有有限个点是“![]() 点”
点”
C.直线![]() 上的所有点都不是“
上的所有点都不是“![]() 点”
点” ![]()
![]()
D.直线![]() 上有无穷多个点(点不是所有的点)是“
上有无穷多个点(点不是所有的点)是“![]() 点”[来源:学。科。网]
点”[来源:学。科。网]
![]()
解析:
本题采作数形结合法易于求解,如图,
设![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴
消去n,整理得关于x的方程![]() (1)
(1)
∵![]() 恒成立,[来源:学。科。网Z。X。X。K]
恒成立,[来源:学。科。网Z。X。X。K]
∴方程(1)恒有实数解,∴应选A.

练习册系列答案
相关题目
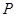 在直线
在直线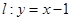 上,若存在过
上,若存在过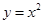 于
于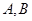 两点,且
两点,且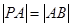 ,则称点
,则称点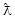 点”,那么下列结论中正确的是( )
点”,那么下列结论中正确的是( )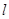 上的所有点都是“
上的所有点都是“ 在直线
在直线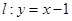 上,若存在过
上,若存在过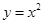 于
于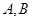 两点,且
两点,且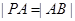 ,则称点
,则称点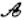 点”,那么下列结论中正确的是( )
点”,那么下列结论中正确的是( ) 上的所有点都是“
上的所有点都是“