题目内容
在平面直角坐标系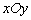 中,从曲线
中,从曲线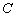 上一点
上一点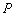 做
做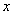 轴和
轴和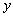 轴的垂线,垂足分别为
轴的垂线,垂足分别为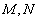 ,点
,点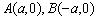 (
( 为常数),且
为常数),且 (
(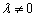 )
)
(1)求曲线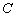 的轨迹方程,并说明曲线
的轨迹方程,并说明曲线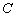 是什么图形;
是什么图形;
(2)当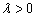 且
且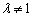 时,将曲线
时,将曲线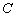 绕原点逆时针旋转
绕原点逆时针旋转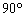 得到曲线
得到曲线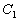 ,曲线
,曲线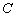 与曲线
与曲线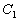 四个交点按逆时针依次为
四个交点按逆时针依次为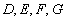 ,且点
,且点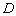 在一象限
在一象限
①证明:四边形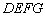 为正方形; ②若
为正方形; ②若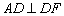 ,求
,求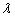 值.
值.
(1)设 ,所以
,所以 ,由
,由 得
得
①当 时,曲线
时,曲线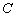 是焦点在
是焦点在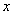 轴的双曲线;
轴的双曲线;
②当 时,曲线
时,曲线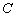 是焦点在
是焦点在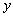 轴的椭圆;
轴的椭圆;
③当 时,曲线
时,曲线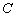 是圆;
是圆;
④当 时,曲线
时,曲线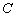 是焦点在
是焦点在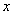 轴的椭圆; ………6分
轴的椭圆; ………6分
(2)①当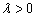 且
且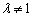 时,曲线
时,曲线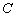 是椭圆,曲线
是椭圆,曲线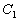 方程为
方程为 ,设
,设
所以两曲线四个交点坐标 ,所以四边形
,所以四边形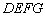 为正方形; ………9分
为正方形; ………9分
②设 ,当
,当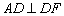 时,
时, 且
且
解得 . ………12分
. ………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“ ”是“数列{an}为等比数列”的( )
”是“数列{an}为等比数列”的( )
|
| A. | 充分不必要条件 | B. | 必要不充分条件 |
|
| C. | 充要条件 | D. | 既不充分也不必要条件 |

 的最小值是 .
的最小值是 . =m
=m ,
, =n
=n (m•n≠0),若
(m•n≠0),若 ∥
∥ ,则
,则 =___________________.
=___________________. 满足
满足 ,则复数
,则复数 的图象向左平移
的图象向左平移 个单位后关于原点对称,则函数
个单位后关于原点对称,则函数 在
在 上的最小值为
上的最小值为 B.
B. C.
C. D.
D.

 满足
满足 ,则
,则 中,⊿
中,⊿ 是等边三角形,
是等边三角形, 是以
是以 为斜边的等腰直角三角形.
为斜边的等腰直角三角形. ,求三棱锥
,求三棱锥