题目内容
(2012•江苏)在平面直角坐标系xOy中,若双曲线
-
=1的离心率为
,则m的值为
| x2 |
| m |
| y2 |
| m2+4 |
| 5 |
2
2
.分析:由双曲线方程得y2的分母m2+4>0,所以双曲线的焦点必在x轴上.因此a2=m>0,可得c2=m2+m+4,最后根据双曲线的离心率为
,可得c2=5a2,建立关于m的方程:m2+m+4=5m,解之得m=2.
| 5 |
解答:解:∵m2+4>0
∴双曲线
-
=1的焦点必在x轴上
因此a2=m>0,b2=m2+4
∴c2=m+m2+4=m2+m+4
∵双曲线
-
=1的离心率为
,
∴
=
,可得c2=5a2,
所以m2+m+4=5m,解之得m=2
故答案为:2
∴双曲线
| x2 |
| m |
| y2 |
| m2+4 |
因此a2=m>0,b2=m2+4
∴c2=m+m2+4=m2+m+4
∵双曲线
| x2 |
| m |
| y2 |
| m2+4 |
| 5 |
∴
| c |
| a |
| 5 |
所以m2+m+4=5m,解之得m=2
故答案为:2
点评:本题给出含有字母参数的双曲线方程,在已知离心率的情况下求参数的值,着重考查了双曲线的概念与性质,属于基础题.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
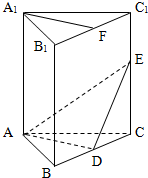 (2012•江苏)如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证:
(2012•江苏)如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证: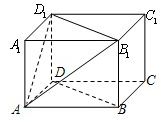 (2012•江苏)如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A-BB1D1D的体积为
(2012•江苏)如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A-BB1D1D的体积为