题目内容
5.设向量$\overrightarrow{a}$,$\overrightarrow{b}$是相互垂直的单位向量,向量λ$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$垂直,则实数λ=2.分析 根据向量垂直,令数量积为零列方程解出.
解答 解:∵向量$\overrightarrow{a}$,$\overrightarrow{b}$是相互垂直的单位向量,
∴$\overrightarrow{a}•\overrightarrow{b}$=0,${\overrightarrow{a}}^{2}={\overrightarrow{b}}^{2}=1$.
∵λ$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$垂直,
∴(λ$\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{b}$)=λ-2=0.
解得λ=2.
故答案为2.
点评 本题考查了平面向量垂直与数量积的关系,属于基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
13.定义运算$|{\begin{array}{l}a&b\\ c&d\end{array}}|?|{\begin{array}{l}e\\ f\end{array}}|=|{\begin{array}{l}{ae-bf}\\{ce-df}\end{array}}|$,例如$|{\begin{array}{l}1&2\\ 3&4\end{array}}|?|{\begin{array}{l}5\\ 6\end{array}}|=|{\begin{array}{l}{-7}\\{-9}\end{array}}|$.若已知$α+β=π,α-β=\frac{π}{2}$,则$|{\begin{array}{l}{sinα}&{cosα}\\{cosα}&{sinα}\end{array}}|?|{\begin{array}{l}{cosβ}\\{sinβ}\end{array}}|$=( )
| A. | $|{\begin{array}{l}0\\ 1\end{array}}|$ | B. | $|{\begin{array}{l}1\\ 0\end{array}}|$ | C. | $|{\begin{array}{l}0\\ 0\end{array}}|$ | D. | $|{\begin{array}{l}1\\{-1}\end{array}}|$ |
20.设a,b都是不等于1的正数,则“loga3<logb3”是“3a>3b>3”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
10.下列说法正确的是( )
| A. | 对立事件一定是互斥事件事件,互斥事件不一定是对立事件 | |
| B. | A、B同时发生的概率一定比A、B中恰有一个发生的概率小 | |
| C. | 若P(A∪B)=P(A)+P(B)=1,则事件A与B是互斥且对立事件 | |
| D. | 事件A、B中至少有一个发生的概率一定比A、B中恰有一个发生的概率大 |
14.从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表,如下:
(1)根据频数分布表计算苹果的重量在[90,95)的频率;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量之差的绝对值大于5的概率.
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | x | 10 | 20 | 15 |
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量之差的绝对值大于5的概率.
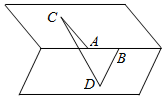 如图,已知在一个二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2$\sqrt{17}$cm,则这个二面角的度数为60°.
如图,已知在一个二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2$\sqrt{17}$cm,则这个二面角的度数为60°.