题目内容
【题目】已知椭圆![]() :
:![]() 的一个焦点
的一个焦点![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)直线![]() 平行于直线
平行于直线![]() (
(![]() 坐标原点),且与椭圆
坐标原点),且与椭圆![]() 交于
交于![]() ,
,![]() 两个不同的点,若
两个不同的点,若![]() 为钝角,求直线
为钝角,求直线![]() 在
在![]() 轴上的截距
轴上的截距![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) ![]() ; (Ⅱ)
; (Ⅱ)![]() 。
。
【解析】
(Ⅰ)由焦点坐标确定出c的值,根据椭圆的性质列出a与b的方程,再将M点坐标代入椭圆方程列出关于a与b的方程,联立求出a与b的值,确定出椭圆方程即可;
(Ⅱ)设直线l方程为![]() ,A(x1,y1)、B(x2,y2),联立l与椭圆方程,消去y得到关于x的一元二次方程,利用韦达定理表示出x1+x2与x1x2,根据∠AOB为钝角,得到
,A(x1,y1)、B(x2,y2),联立l与椭圆方程,消去y得到关于x的一元二次方程,利用韦达定理表示出x1+x2与x1x2,根据∠AOB为钝角,得到![]()
![]() 0,即x1x2+y1y2<0,即可确定出m的范围;
0,即x1x2+y1y2<0,即可确定出m的范围;
(Ⅰ)由已知![]() ,则
,则![]() ①
①
又点![]() 在椭圆
在椭圆![]() 上,
上,
所以![]() ②
②
由①②解得![]() (
(![]() 舍去),
舍去),![]() .
.
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)由直线![]() 平行于
平行于![]() 得直线
得直线![]() 的斜率为
的斜率为![]() ,又
,又![]() 在
在![]() 轴上的截距
轴上的截距![]() ,
,
故![]() 的方程为
的方程为![]() .
.
由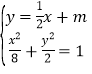 得
得![]() ,又线与椭圆
,又线与椭圆![]() 交于
交于![]() ,
,![]() 两个不同的点,
两个不同的点,
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
所以![]() ,于是
,于是![]() .
.
![]() 为钝角等价于
为钝角等价于![]() ,且
,且![]() ,则
,则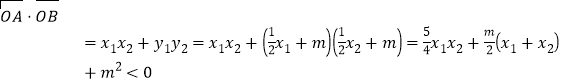 ,
,
即![]() ,又
,又![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
【题目】已知从甲地到乙地的公路里程约为240(单位:km).某汽车每小时耗油量Q(单位:L)与速度x(单位:![]() )(
)(![]() )的关系近似符合以下两种函数模型中的一种(假定速度大小恒定):①
)的关系近似符合以下两种函数模型中的一种(假定速度大小恒定):①![]() ,②
,②![]() ,经多次检验得到以下一组数据:
,经多次检验得到以下一组数据:
x | 0 | 40 | 60 | 120 |
Q | 0 |
|
| 20 |
(1)你认为哪一个是符合实际的函数模型,请说明理由;
(2)从甲地到乙地,这辆车应以多少速度行驶才能使总耗油量最少?

