题目内容
若方程 2x+
-a=0有负数根,则实数a的取值范围是
| x-2 | x-1 |
(1,3)
(1,3)
.分析:先将方程 2x+
-a=0化为:2x=a-
.我们在同一坐标系画出函数y=2x和 y=a-
两个图象,利用数形结合思想,易得实数a的取值范围.
| x-2 |
| x-1 |
| x-2 |
| x-1 |
| x-2 |
| x-1 |
解答: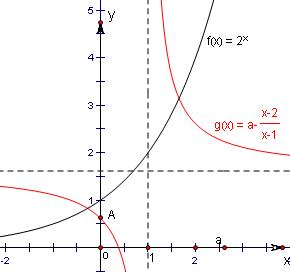 解:方程 2x+
解:方程 2x+
-a=0化为:2x=a-
.
在同一坐标系画出y=2x和 y=a-
两个图象
若方程 2x+
-a=0有负数根,
则y=2x和 y=a-
两个图象在y轴的左侧有交点,
须
,解得1<a<3.
故实数a的取值范围是(1,3).
故答案为:(1,3).
 解:方程 2x+
解:方程 2x+| x-2 |
| x-1 |
| x-2 |
| x-1 |
在同一坐标系画出y=2x和 y=a-
| x-2 |
| x-1 |
若方程 2x+
| x-2 |
| x-1 |
则y=2x和 y=a-
| x-2 |
| x-1 |
须
|
故实数a的取值范围是(1,3).
故答案为:(1,3).
点评:本题考查的知识点是函数的零点与方程根的关系,及函数图象,其中在同一坐标中,画出y=2x和 y=a-
两个图象,结合数形结合的思想得到答案,是解答本题的关键.
| x-2 |
| x-1 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的根分别为p和q,若函数f(x)=(x+p)(x+q)+2,则
的根分别为p和q,若函数f(x)=(x+p)(x+q)+2,则