题目内容
在 中,
中, 分别为角
分别为角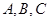 所对的三边,
所对的三边, ,
,
(Ⅰ)求角 ;
;
(Ⅱ)若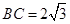 ,角
,角 等于
等于 ,周长为
,周长为 ,求函数
,求函数 的取值范围.
的取值范围.
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
【解析】
试题分析:(Ⅰ)根据题目条件,容易联想到余弦定理,求出角 ; (Ⅱ)求函数
; (Ⅱ)求函数 的取值范围,这是一个函数的值域问题,需先找出函数关系式,因此要先把各边长求出来,或用
的取值范围,这是一个函数的值域问题,需先找出函数关系式,因此要先把各边长求出来,或用 表示出来,方法是利用正弦定理来沟通三角形的边角关系,求出函数关系式后,不要忘记求函数的定义域,根据函数定义域去求函数的值域,这显然又是一个三角函数的值域问题,可化为
表示出来,方法是利用正弦定理来沟通三角形的边角关系,求出函数关系式后,不要忘记求函数的定义域,根据函数定义域去求函数的值域,这显然又是一个三角函数的值域问题,可化为 的类型求解.
的类型求解.
试题解析:(Ⅰ)由 ,得
,得 ,
,
 3分
3分
又 ,
,  6分
6分
(Ⅱ)

同理: 9分
9分



故 ,
, ,
, . 12分
. 12分
考点:正弦定理、余弦定理、三角函数的值域.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 中,
中, 分别为角
分别为角 所对的边,向量
所对的边,向量 ,
,
 ,且
,且 垂直.
垂直. 的大小;
的大小; 的平分线
的平分线 交
交 于点
于点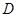 ,且
,且 ,设
,设 ,试确定
,试确定 关于
关于 的函数式,并求边
的函数式,并求边 长的取值范围.
长的取值范围.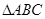 中,
中, 分别为角
分别为角 所对的三边,已知
所对的三边,已知 .
. 的值;
的值; ,
, ,求
,求 的长.
的长.