题目内容
解下列不等式
(1)
>1;
(2)
.
(1)
| 2-x |
| x+4 |
(2)
|
分析:(1)将分式不等式转化为整式不等式进行求解即可.
(2)利用一元二次不等式和绝对值不等式的解法解不等式即可.
(2)利用一元二次不等式和绝对值不等式的解法解不等式即可.
解答:解:(1)∵
>1,
∴
-1=
>0,即
<0,
即2(x+1)(x+4)<0,
解得-4<x<-1,即不等式的解集为(-4,-1).
(2)由
,得
,
即
,
解得-2<x<1或2<x<4.
即不等式的解集为{x|-2<x<1或2<x<4}.
| 2-x |
| x+4 |
∴
| 2-x |
| x+4 |
| -2x-2 |
| x+4 |
| 2x+2 |
| x+4 |
即2(x+1)(x+4)<0,
解得-4<x<-1,即不等式的解集为(-4,-1).
(2)由
|
|
即
|
解得-2<x<1或2<x<4.
即不等式的解集为{x|-2<x<1或2<x<4}.
点评:本题主要考查不等式的解法,要求熟练掌握分式不等式,绝对值不等式以及一元二次不等式的解法.

练习册系列答案
相关题目
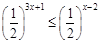 ; (2)
log73x < log7(x2-4).
; (2)
log73x < log7(x2-4).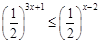 ; (2) log73x
< log7(x2-4).
; (2) log73x
< log7(x2-4).