题目内容
在下列条件中，M与A、B、C一定共面的是（ ）
分析：利用空间向量基本定理，进行验证，对于C，可得
，
，
为共面向量，从而可得M、A、B、C四点共面
| MA |
| MB |
| MC |
解答：解：C中，由
+
+
=
，得
=-
-
，则
，
，
为共面向量，即M、A、B、C四点共面．
对于A，
+
+
=
-
+
-
+
-
=
+
+
-3
≠
，∴M、A、B、C四点不共面
对于B，∵
+
+
≠1，∴M、A、B、C四点不共面
对于D，∵
+
+
+
=
，
=-（
+
+
），系数和不为1，∴M、A、B、C四点不共面
故选C．
| MA |
| MB |
| MC |
| 0 |
| MA |
| MB |
| MC |
| MA |
| MB |
| MC |
对于A，
| MA |
| MB |
| MC |
| OA |
| OM |
| OB |
| OM |
| OC |
| OM |
| OA |
| OB |
| OC |
| OM |
| 0 |
对于B，∵
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 2 |
对于D，∵
| OM |
| OA |
| OB |
| OC |
| 0 |
| OM |
| OA |
| OB |
| OC |
故选C．
点评：本题考查空间向量基本定理，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
=2
-
-
=
+
+
+
+
=
+
+
+
=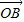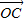
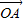
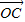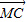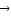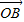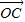