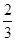题目内容
若n∈N*,且n为奇数,则6n+C
•6n-1+C
•6n-2+…+C
•6被8除所得的余数是______.
| 1n |
| 2n |
| n-1n |
法一:根据题意,6n+Cn1•6n-1+Cn2•6n-2+…+Cnn-1•6
=6n+Cn1•6n-1+Cn2•6n-2+…+Cnn-1•6+Cnn-1
=(6+1)n-1=7n-1=(8-1)n-1
=Cn0•8n-Cn1•8n-1+…+(-1)n-1Cnn-1•8+(-1)nCnn-1
又由n为奇数,则6n+Cn1•6n-1+Cn2•6n-2+…+Cnn-1•6-1=Cn0•8n-Cn1•8n-1+…+(-1)n-1Cnn-1•8-2,
且Cn0•8n-Cn1•8n-1+…+(-1)n-1Cnn-1•8可以被8整除,
则6n+Cn1•6n-1+Cn2•6n-2+…+Cnn-1•6被8除所得的余数是6;
法二,根据题意,n∈N*,且n为奇数,
在6n+Cn1•6n-1+Cn2•6n-2+…+Cnn-1•6中,令n=1,可得6n+Cn1•6n-1+Cn2•6n-2+…+Cnn-1•6=6,
6n+Cn1•6n-1+Cn2•6n-2+…+Cnn-1•6被8除所得的余数是6.
故答案为:6.
=6n+Cn1•6n-1+Cn2•6n-2+…+Cnn-1•6+Cnn-1
=(6+1)n-1=7n-1=(8-1)n-1
=Cn0•8n-Cn1•8n-1+…+(-1)n-1Cnn-1•8+(-1)nCnn-1
又由n为奇数,则6n+Cn1•6n-1+Cn2•6n-2+…+Cnn-1•6-1=Cn0•8n-Cn1•8n-1+…+(-1)n-1Cnn-1•8-2,
且Cn0•8n-Cn1•8n-1+…+(-1)n-1Cnn-1•8可以被8整除,
则6n+Cn1•6n-1+Cn2•6n-2+…+Cnn-1•6被8除所得的余数是6;
法二,根据题意,n∈N*,且n为奇数,
在6n+Cn1•6n-1+Cn2•6n-2+…+Cnn-1•6中,令n=1,可得6n+Cn1•6n-1+Cn2•6n-2+…+Cnn-1•6=6,
6n+Cn1•6n-1+Cn2•6n-2+…+Cnn-1•6被8除所得的余数是6.
故答案为:6.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 (n=1,2,3,4),其中a是常数,则P(
(n=1,2,3,4),其中a是常数,则P( <X<
<X< )的值为( )
)的值为( )