题目内容
11.已知点M与两个定点O(0,0),A(3,0)的距离之比为2,则M点轨迹方程是(x-4)2+y2=4.分析 设出M的坐标,直接由M与两个定点O(0,0),A(3,0)的距离之比为2,列式整理得方程.
解答 解:设M(x,y),由点M与两个定点O(0,0),A(3,0)的距离之比为2,得
$\frac{\sqrt{{x}^{2}+{y}^{2}}}{\sqrt{(x-3)^{2}+{y}^{2}}}$=2,整理得:(x-4)2+y2=4.
∴点M的轨迹方程是(x-4)2+y2=4.
故答案为:(x-4)2+y2=4.
点评 本题考查了轨迹方程的求法,考查了两点间的距离公式,是中低档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
19.执行如图的程序框图,若输人a=319,b=87,则输出的a是( )


| A. | 19 | B. | 29 | C. | 57 | D. | 76 |
20.某银行柜台设有一个服务窗口,假设顾客办理业务所需的时间互相独立,且都是整数分钟,对以往顾客办理业务所需的时间Y统计结果如下:
从第一个顾客开始办理业务时计时,据上表估计第三个顾客等待不超过4分钟就开始办理业务的概率为( )
| 办理业务所需的时间Y/分 | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
| A. | 0.22 | B. | 0.24 | C. | 0.30 | D. | 0.31 |
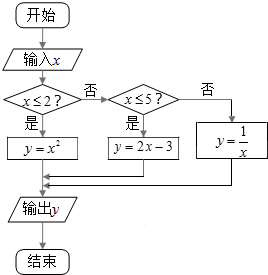 如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值.
如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值.