题目内容
(本小题满分14分)
已知函数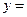
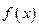 的定义域为R, 且对于任意
的定义域为R, 且对于任意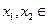 R,存在正实数
R,存在正实数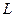 ,使得
,使得
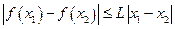 都成立.
都成立.
若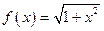 ,求
,求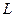 的取值范围;
的取值范围;
当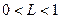 时,数列
时,数列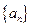 满足
满足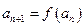 ,
,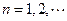 .
.
证明: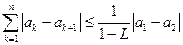 ;
;
令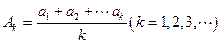 ,证明:
,证明: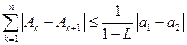 .
.
已知函数
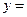
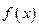 的定义域为R, 且对于任意
的定义域为R, 且对于任意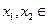 R,存在正实数
R,存在正实数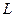 ,使得
,使得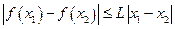 都成立.
都成立.若
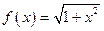 ,求
,求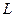 的取值范围;
的取值范围;当
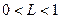 时,数列
时,数列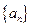 满足
满足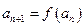 ,
,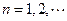 .
.证明:
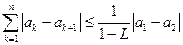 ;
;令
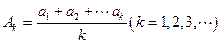 ,证明:
,证明: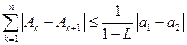 .
.(本小题主要考查函数、数列求和、绝对值不等式等知识, 考查化归与转化的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识)
证明:对任意
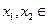 R,有
R,有

 . …… 2分
. …… 2分由
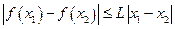 ,即
,即
 .
.当
 时,得
时,得 .
. 且
且 ,
,∴
 . …… 4分
. …… 4分∴要使
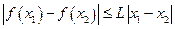 对任意
对任意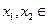 R都成立,只要
R都成立,只要 .
.当
 时,
时, 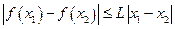 恒成立.
恒成立.∴
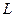 的取值范围是
的取值范围是 . …… 5分
. …… 5分(2) 证明:①∵
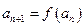 ,
,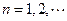 ,
,故当
 时,
时,
 . …… 6分
. …… 6分∴

 …… 7分
…… 7分 . …… 8分
. …… 8分∵
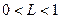 ,
,∴
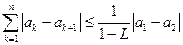
 当
当 时,不等式也成立
时,不等式也成立 . …… 9分
. …… 9分②∵
 ,
,∴



 .
.…… 11分
∴






 . ……14分
. ……14分略

练习册系列答案
相关题目

 ,则下列不等式一定成立的是
,则下列不等式一定成立的是



 ,
, 满足
满足 则
则 的最大值为_________.
的最大值为_________. 函数
函数
 时,求函数
时,求函数 的定义域;
的定义域;  的取值范围。
的取值范围。 2,则3a+3b的最小值是
2,则3a+3b的最小值是  C
C
 .2
.2 D.2
D.2

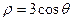 ,则圆截直线
,则圆截直线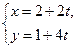 (
(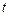 是参数
是参数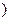 所得的
所得的 弦长为 ;
弦长为 ;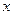 的不等式
的不等式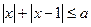 有解,则实数
有解,则实数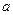 的取值范围是 。
的取值范围是 。 <
< <0,则下列不等式:①a+b<ab,②|a|>|b|,③a<b,④
<0,则下列不等式:①a+b<ab,②|a|>|b|,③a<b,④ >2中正确的不等式序号是 ( )
>2中正确的不等式序号是 ( )