Question

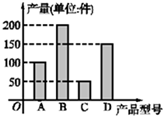（2012•房山区二模）某工厂2011年生产的A，B，C，D四种型号的产品产量用条形图表示如图，现用分层抽样的方法从中选取50件样品参加今年五月份的一个展销会．
（I）问A，B，C，D型号的产品各抽取多少件？
（II）从50件样品中随机地抽取2件，求这2件产品恰好是不同型号产品的概率；
（III） 50件样品中，从A，C型号的产品中随机抽取3件，用X表示抽取的A种型号产品的件数，求X的分布列和数学期望．

Answer 1

分析：（I）从条形图上可知，共生产产品有50+100+150+200=500（件），确定样品比，即可求A，B，C，D型号的产品各抽取的件数；
（II）求出从50件样品中随机地抽取2件的方法数，再求这2件产品恰好是不同型号产品的方法数，即可概率；
（III）确定X的取值，求出相应的概率，即可得到分布列与期望．

解答：解：（I）从条形图上可知，共生产产品有50+100+150+200=500（件），样品比为

50

500

=

1

10

，
所以A，B，C，D四种型号的产品分别取

1

10

×100=10，

1

10

×200=20，

1

10

×50=5，

1

10

×150，
即样本中应抽取A产品10件，B产品20件，C产品5件，D产品15件．…（3分）
（II）从50件产品中任取2件共有

C

2 50

=1225种方法，
2件恰为同一产品的方法数为

C

2 10

+

C

2 20

+

C

2 5

+

C

2 15

=350种，
所以2件恰好为不同型号的产品的概率为1-

350

1225

=

5

7

．…（6分）
（III）X的可能取值为0，1，2，3，则P（X=0）=

C 3 5

C 3 15

=

10

455

，P（X=1）=

C 1 10 C 2 5

C 3 15

=

100

455

，P（X=2）=

C 2 10 C 1 5

C 3 15

=

225

455

，P（X=3）=

C 3 10

C 3 15

=

120

455

，…（9分）
故X的分布列为

P	0	1	2	3
X	10 455	100 455	225 455	120 455

所以EX=0×

10

455

+1×

100

455

+2×

225

455

+3×

120

455

=2 …（13分）

点评：本题考查条形图，考查概率的计算，考查离散型随机变量的分布列与期望，正确求概率是关键．